13. Reaktor v prevádzkových podmienkach.

Ak má reaktor pracovať v ustálenom stave, musí byť efektívny multiplikačný koeficient po celú túto dobu rovný jednej. Napriek tomu, že reaktor bol vypočítaný tak, aby bol práve kritický, nezostane zachovaný efektívny multiplikačný koeficient rovný jednej ľubovoľne dlhú dobu. Na efektívny multiplikačný koeficient nepriaznivo pôsobí viacero činiteľov, ako sú: teplota, vyhorenie paliva, otrava spôsobená produktmi štiepenia a hromadenie strusky. Všetky tieto činitele zmenšujú postupne keff. Pri práci reaktora v aktívnej zóne ubúda jadrového paliva, takže pre zabezpečenie dlhodobej činnosti reaktora je potrebné použiť viac paliva ako je minimálne množstvo potrebné na vytvorenie kritickej sústavy. Jadrové palivo je v aktívnej zóne len čiastočne využívané, a to z 10 - 15%, tomuto tiež hovoríme vyhorenie paliva v reaktore. Na hodnotu vyhorenia vplývajú nasledovné činitele : tvar a konštrukcia reaktora, chemické zloženie konštrukčných materiálov, odolnosť palivových článkov voči účinkom žiarenia.

Pri spúšťaní reaktora musí byť v AZ umiestnené viac štiepneho materiálu, a to o hodnotu viazanej reaktivity teplotnými zmenami, vyhorenia paliva a hromadenia štiepnych produktov za dobu nachádzania sa palivového článku v AZ, čo zhruba predstavuje 18 - 25% štiepneho materiálu naviac. Toto množstvo jadrového paliva nahrádza úbytok reaktivity počas činnosti reaktora.

13.1 Vplyv teplotných zmien na reaktivitu reaktora

Tepelná energia uvoľňovaná v jadrovom reaktore pri štiepení paliva spôsobuje rast teplôt jednotlivých zložiek aktívnej zóny. Pritom sa menia jadrovo-fyzikálne konštanty závislé na teplote a vplyvom tepelnej dilatácie sa zmenšuje hustota materiálov. V malej miere sa mení geometria a rozmery aktívnej zóny. Všetky tieto zmeny majú vplyv na neutrónovú bilanciu v aktívnej zóne a prejavujú sa zmenou reaktivity štiepneho systému.

Z hľadiska stability systému má veľký význam, či je rast teploty reaktora spojený s kladnou alebo zápornou reaktivitou. Vo väčšine reaktorov zodpovedá rastúcej teplote záporná reaktivita, takýto reaktor je teplotne stabilný.

Tepelná energia uvoľňovaná v jadrovom reaktore pri štiepení jadier spôsobuje narastanie teploty jednotlivých častí aktívnej zóny. Pritom sa menia:

 a) jadrovo fyzikálne konštanty závislé od teploty

 b) hustota látok sa zmenšuje

 c) nepatrne sa zväčšujú rozmery AZ.

Všetky tieto zmeny majú za následok zmenu množivých vlastností AZ, t.j. zmenu , respektívne reaktivity . Z hľadiska stability systému je dôležité, či nárast teploty privodí zväčšenie alebo zmenšenie reaktivity. Vo väčšine reaktorov odpovedá rastúcej teplote záporná reaktivita, reaktor je teplotne stabilný.

13.1.1 Teplotné koeficienty reaktivity

Teplotný koeficient reaktivity je definovaný ako: zmena reaktivity odpovedajúca jednotkovej zmene teploty i-tej zložky aktívnej zóny, tj:

                                                                                          (13.1)

V rozmedzí teplôt, ktoré podstatne nevplývajú na geometriu systému, je možné vyjadriť celkový účinok teplotných zmien na reaktivitu ako súčet teplotných efektov reaktivity vážených cez objem Vi

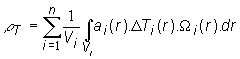                                              (13.2)

kde  - teplotný rozdiel, alebo odchýlka teploty i-tej zložky AZ v mieste r od hodnoty odpovedajúcej stavu

 - normovaná váhová funkcia – vyjadruje skutočnosť, že teplotné zmeny spôsobujúce zmenu fyzikálnych vlastností v rôznych častiach AZ,. nemusia mať vždy rovnaký vplyv na reaktivitu reaktora.

Často je možné bez ujmy na presnosti zanedbať priestorovú zmenu teplotných koeficientov reaktivity a použiť vhodne zostredovaných hodnôt . Potom platí:

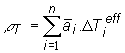                                                                           (13.3)

kde teplotný rozdiel je možné stanoviť nasledovne:

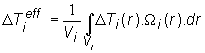                                                       (13.4)

Teplotný koeficient reaktivity môžeme vyjadriť ako súčet jadrovej a hustotnej zložky.

Jadrová zložka vyjadruje vplyv teplotných zmien na mikroskopické účinné prierezy. Najväčší vplyv má spravidla:

1; zmena teploty moderátora, zvýšeniu teploty zodpovedá posun spektra tepelných neutrónov k vyšším hodnotám, tomu zodpovedá zmena stredovaných mikroskopických účinných prierezov.

2; zmena teploty paliva, zvýšením teploty paliva sa uplatní Dopplerov efekt, zníži sa pravdepodobnosť úniku rezonančnému záchytu.

 Hustotná zložka vyjadruje vplyv tepelnej rozťažnosti na hustotu materiálu. V dôsledku zmeny hustoty jadier sa menia aj makroskopické účinné prierezy. Vplyv jednotlivých javov na reaktivitu závisí od použitých materiálov moderátora, chladiva a paliva ako aj od ich usporiadania v AZ.

13.1.2 Teplotné koeficienty reaktivity veľkého tepelného reaktora.

V heterogénnom reaktore sú od seba priestorovo oddelené tri základné časti AZ, palivo, moderátor a chladivo, z toho vyplýva aj rozdielnosť ich teplôt. Nech T0, T1 a T2 sú teploty paliva, moderátora a chladiva, potom môžeme definovať teplotné koeficienty jednotlivých zložiek AZ nasledovne:

                                                                                        (13.5)

                                                                                          (13.6)

                                                                                         (13.7)

Pre veľký reaktor je podľa jednoskupinovej teórie efektívny multiplikačný koeficient keff určený vzťahom:

                                                                            (13.8)

Reaktivita je potom určená nasledovne:

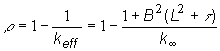                                                   (13.9)

Veličiny , B2, L2,  sú obecne funkciami teploty. Teplotný koeficient je možné stanoviť ako totálny diferenciál reaktivity  podľa teploty T, potom platí:

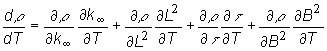                                    (13.10)

Z výrazu (13.9) pre reaktivitu veľkého reaktora 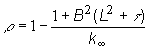 určíme jednotlivé príspevky k totálnemu diferenciálu (13.10):

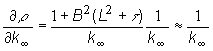                                                                (13.11)

 Pred zmenou teploty reaktor pracoval na ustálenej výkonovej hladine, efektívny multiplikačný koeficient bol rovný jednej. Po zmene teploty v sa úmerne zmenia štiepne vlastnosti prostredia , čo sa prejaví ako malá zmena keff. V menovateli (13.11) sa súčin  sa preto líši od  o zanedbateľne malú hodnotu lebo keff sa veľmi málo líši od 1, tj. keff » 1. Preto sa derivácia reaktivity vo výraze (13.11) rovná obrátenej hodnote . Integráciou (13.11) potom obdržíme vzťah pre reaktivitu ako . V ďalšom tento vzťah použijeme pri určení teplotných koeficientov.

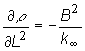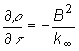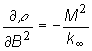, ,                                                   (13.12)

Dosadením za , potom  má tvar:

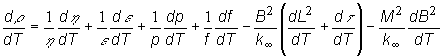       (13.13)

Tento výraz umožňuje určiť teplotný koeficient reaktora, v ktorom sú teploty všetkých zložiek rovnaké. V heterogénnom reaktore je nutné derivovať podľa teploty všetkých zložiek AZ, ktoré pri teplotnej zmene môžu ovplyvniť reaktivitu reaktora. Teplotný koeficient reaktivity i-tej zložky reaktora potom je:

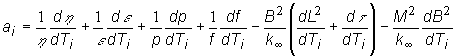   (13.14)

13.1.3 Dopplerov efekt

Teplota paliva je priamo spojená s výkonom reaktora, pri vzraste výkonu rastie aj teplota paliva. Teplota prostredia je mierou tepelného pohybu jeho atómov. Zvýšenie teploty paliva sa teda prejaví na zvýšení rýchlosti tepelného pohybu aj jadier 238U a

tým aj na pravdepodobnosti úniku rezonančnému jadrami 238U. Pravdepodobnosť úniku rezonančnému záchytu neutrónov jadrami 238U závisí od relatívnej rýchlosti neutrónov a jadier 238U. Zvýšenie tepelného pohybu sa potom prejaví tým, že sa rozšíri rezonančná hladina jadra a zníži sa jej maximum, čo je zrejme z obr13.1, pričom sa plocha pod rezonančnou čiarou nemení. Pretože efektívny rezonančný integrál (10.11) obsahuje mikroskopický účinný prierez absorpcie neutrónov v 238U aj menovateli, je aj  závislé od teploty. Takto je potom závislá od teploty aj pravdepodobnosť úniku rezonančnému zachyteniu:

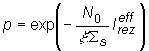                                                                                (13.15)

Efektívny rezonančný integrál má podľa uvedeného vzťahu tvar:

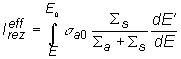                                                                        (13.16)

Z výrazu (13.16) pre  je zrejmé, že mikroskopický účinný prierez absorpcie v 238U  je tiež obsiahnutý aj v menovateli, je teda  závislé od teploty.

Jadrový teplotný koeficient veličiny p je určený hlavne zmenou  v dôsledku Dopplerovho efektu. Pri zmene teploty paliva T0 podľa (13.14) pre teplotou vyvolanú zmenu reaktivity potom platí:

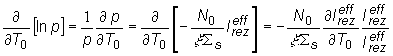                   (13.17)

Keďže palivo je tuhá látka, môžeme pri derivovaní (13.14) považovať N0 koncentráciu jadier 238U ako aj makroskopický účinný prierez rozptylu Ss za nemenné v rozsahu zmien teploty T0.Úpravou (13.17) obdržíme jadrový teplotný koeficient veličiny p v tvare:

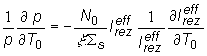                                                                  (13.18)

Prvý člen na pravej strane (13.18) prestavuje lnp, preto ďalej platí:

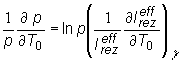                                                                         (13.19)

Index g označuje hustotu paliva, ktorú pri zmene jeho teploty považujeme za nemennú. Veličina v zátvorke (13.19) je jadrový teplotný koeficient efektívneho rezonančného integrálu, ktorý označujeme . Potom má (13.19) nasledovný tvar:

                                                                                          (13.20)

Jadrový teplotný koeficient reaktivity efektívneho rezonančného integrálu je rovný:

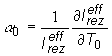                                                                                          (13.21)

Rastúca teplota paliva spôsobuje zväčšenie , preto Dopplerov efekt je vždy záporný. Typická hodnota a0 je u tlakovodných reaktorov rovná 10-4 K-1, teplotný koeficient reaktivity odpovedajúci Dopplerovmu efektu (pri p » 0,9) je potom rovný –10-5 K-1. Zvýšenie teploty paliva spojené s prudkým rastom výkonu reaktora sa prejaví zápornou reaktivitou, ktorá môže podstatne obmedziť alebo utlmiť rozbeh reťazovej reakcie štiepenia.

13.1.4 Teplotné koeficienty reaktivity tlakovodných reaktorov

V tlakovodných reaktoroch je chladivo súčasne moderátorom. Preto v takomto reaktore nám vplýva na reaktivitu iba zmena teploty paliva a moderátora. Pri teplotných zmenách moderátora prevláda vplyv zmeny hustoty vody, pri zmenách teploty paliva je dominujúcou zložka jadrového teplotného koeficienta reaktivity.

Zmena hustoty vody má vplyv predovšetkým na súčiniteľ využitia tepelných neutrónov f a pravdepodobnosť úniku rezonančnému záchytu p. Teplotný koeficient reaktivity moderátora je potom rovný:

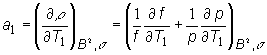                                                               (13.22)

Zmena teploty moderátora nespôsobí pozorovateľnú zmenu rozmerov reaktora a zmenu teploty neutrónového plynu, preto únik neutrónov charakterizovaný geometrickým parametrom B2 a mikroskopické účinné prierezy s sú pri derivácii nemenné. Hustotný koeficient veličiny f je kladný, pretože zmena počtu jadier vodíka NH v jednotke objemu je pri teplotných zmenách úmerná zmene hustoty vody , čo sa prejaví na makroskopickom účinnom priereze absorpcie v moderátore. Relatívna zmena hustoty jadier a makroskopického účinného prierezu absorpcie je daná vzťahom:

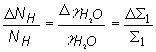                                                                                          (13.23)

S rastúcou teplotou sa znižuje hustota , rastie objem vody a jej prebytočná časť je vytlačená z aktívnej zóny. Tým sa znižuje parazitná absorpcia neutrónov v moderátore. Tento efekt je ešte výraznejší v reaktoroch, ktoré používajú na kompenzáciu reaktivity kyselinu boritú. Čím väčšia je koncentrácia bóru vo vode, tým väčší je kladný hustotný koeficient veličiny f, pretože vytlačením časti vody z AZ, je vytlačená aj časť bóru. Parazitná absorpcia neutrónov v bóre je tiež úmerná pomeru . Znižovanie hustoty vody v dôsledku jej ohrevu, má za následok zníženie spomaľovacej schopnosti moderátora . Tento efekt sa prejaví znížením pravdepodobnosti úniku rezonančnému záchytu p, pretože  vystupuje v menovateli vzťahu:

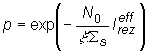
Teplotný koeficient reaktivity moderátora je teda daný ako súčet dvoch členov, z ktorých jeden je kladný a druhý záporný. Nakoľko z hľadiska dynamickej stability reaktora je nežiadúce, aby teplotný koeficient a1 bol kladný, je nutné obmedziť maximálnu koncentráciu bóru v AZ tak, aby a1 bol vždy záporný. V tlakovodných reaktoroch hodnota teplotného koeficienta reaktivity moderátora závisí od teploty a koncentrácie kyseliny boritej cB v moderátore. S rastúcou hodnotou koncentrácie kyseliny boritej klesá absolútna hodnota teplotného koeficienta reaktivity v celom rozsahu teplôt moderátora. Závislosť teplotného koeficienta reaktivity moderátora v

 tlakovodnom reaktore je na obr.13.1. Na obrázku sú uvedené závislosti a1 ako funkcia teploty TM a kyseliny boritej pre koncentrácie: 1-cB=12 g/kg; 2-cB=8g/kg; 3-cB=6g/kg; 4-cB=4g/kg; 5-cB=2g/kg; a 6-cB=0g/kg.


Obr.13.1 Závislosť koeficienta reaktivity moderátora od teploty.

Teplotný koeficient paliva je daný prevažne Dopplerovým efektom:

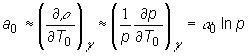                                                        (13.24)

 - konštanta

V tlakovodných reaktoroch dosahuje teplotný koeficient reaktivity paliva hodnotu a0 » -2.10-5 K-1. Celková zmena reaktivity tlakovodných reaktorov pri teplotných zmenách paliva a moderátora je potom rovná:

                                                                         (13.25)

Aj keď teplotný koeficient reaktivity moderátora a1, spravidla o rád prevyšuje teplotný koeficient reaktivity paliva a0, neznamená to, že vplyv teplotných zmien paliva je v každom prípade zanedbateľný. V typickom tlakovodnom reaktore sa teplota vody zvýši zhruba o 250°C a teplota paliva o 1000°C. Reaktivita , ktorú je nutné uvolniť, aby boli vykompenzované zmeny reaktivity vzniknuté ohriatím reaktora, je rovná:

13.1.5 Reaktorové koeficienty reaktivity

Dôležitou charakteristikou energetického jadrového reaktora je reaktivita, odpovedajúca teplotným zmenám v AZ, ku ktorým dochádza pri jednotkovej zmene vstupnej teploty chladiva, výkonu reaktora, hmotnostného prietoku chladiva,alebo tlaku v primárnom okruhu. Podľa príčiny spôsobujúcej zmeny teploty oproti normálnemu stavu môžeme definovať nasledujúce veličiny:

Teplotný koeficient reaktivity vstupnej teploty chladiva je definovaný ako reaktivita , odpovedajúca zmene vstupnej teploty chladiva o 1°C.

                                                                                                   (13.26)

Zmena vstupnej teploty chladiva ovplyvní strednú teplotu chladiva v reaktore, preto sa na zmene reaktivity uplatní hustotný efekt moderátora.

Výkonový koeficient reaktivity aQ, je definovaný ako zmena reaktivity energetického reaktora odpovedajúca zmene výkonu reaktora Q o jednotku výkonu (1kW, 1MW):

                                                                                                    (13.27)

Výkonová zmena spôsobí v prvom rade zmenu teploty paliva a následne aj zmenu teploty chladiva. Na zmenu reaktivity v tomto prípade bude hlavne vplývať Dopplerov efekt na palive.

Koeficient reaktivity prietoku chladiva aG, je definovaný ako zmena reaktivity energetického reaktora odpovedajúca zmene prietoku chladiva  o 1 kg/s:

                                                                                         (13.28)

Zmenená prietočná rýchlosť, pri nezmenenom výkone, bude pôsobiť na strednú teplotu chladiva, preto sa na zmene reaktivity v prejaví hustotný efekt moderátora. Doteraz uvedené reaktorové koeficienty reaktivity sú záporné.

Tlakový koeficient reaktivity ap, je definovaný ako zmena reaktivity energetického reaktora odpovedajúca zmene tlaku p v primárnom okruhu o jednotku (1 MPa):

                                                                                         (13.29)

Meniaci sa tlak v primárnom okruhu sa prejaví na zmene hustoty moderátora, preto sa na zmene reaktivity prejaví hustotný efekt moderátora. Tlakový koeficient reaktivity je kladný. V prípade poklesu tlaku v PO bude klesajúci tlak chladiva viazať určitú časť reaktivity.

Výhodou týchto koeficientov reaktivity je, že sa dajú ľahko zistiť meraním na reaktore.

13.2 Otrava reaktora produktmi štiepenia

Pri štiepení jadier vzniká veľké množstvo rôznych produktov, ktoré sú spravidla  rádioaktívne, preto sa rozpadajú na stabilnejšie jadrá. Niektoré z takto vzniknutých jadier majú veľký účinný prierez absorpcie tepelných neutrónov a negatívne ovplyvňujú bilanciu neutrónov v aktívnej zóne. Pretože produkty rádioaktívneho rozpadu vznikajú aj vtedy, keď sa výkon reaktora zníži, môže koncentrácia týchto absorbátorov vzrastať i po zastavení reaktora a dosiahnuť maxima. Aby bolo možné reaktor spustiť kedykoľvek, je potrebné mať v AZ zásobu reaktivity, ktorá kompenzuje zvýšenú koncentráciu uvedených produktov štiepenia. Obzvlášť významné sú dva izotopy  a , ktorých mikroskopické účinné prierezy sú veľmi veľké. Otravnými nazývame tie produkty štiepenia, ktoré majú veľký mikroskopický účinný prierez absorpcie tepelných neutrónov a súčasne sú nestabilné ( sú rádioaktívne). Skupinu otravných produktov štiepenia tvoria izotopy:. Reprezentantom skupiny otravných produktov štiepenia je, ako už bolo uvedené, . Okrem otravných produktov rozlišujeme aj skupinu štiepnych produktov, ktoré významne vplývajú na bilanciu neutrónov počas prevádzky reaktora. Majú teda veľký mikroskopický účinný prierez absorpcie tepelných neutrónov a sú stabilné, alebo ich polčas premeny je podstatne väčší ako doba pobytu paliva v reaktore. Tieto produkty štiepenia nazývame struskou. Najvýznamnejším zo strusiek je izotop samária .

Podrobnejšie rozoberieme vznik a hromadenie otravného produktu štiepenia .

Pri štiepení  vzniká izotop Telúru  s výťažkom 5,6%, tento je rádioaktívny a rozpadá sa  rozpadom v rozpadovom reťazci:

                    2 min            6,7 h                9,2 h            2.104 r

Okrem toho vzniká  priamo pri štiepení  s výťažnosťou 0,3%. Zo všetkých štiepnych produktov má najväčší účinný prierez pre absorpciu tepelných neutrónov izotop , dosahuje hodnotu 2,65.10-18 cm2. Rozpadová konštanta tohto otravného produktu je rovná = 2,1158.10-5 s-1. Vzhľadom na to, že  má veľké  a pomerne veľkú výťažnosť, môže mať veľký vplyv na bilanciu neutrónov v AZ.

Otravný produkt zaniká prirodzeným rozpadom a absorpciou tepelných neutrónov, pričom vzniká iný izotop, ktorého  je podstatne menšie. Tak napr. z  vzniká , ktorý má = 7.10-24 cm2.

Ak reaktor pracuje dostatočne dlhú dobu na istej úrovni výkonu, úmerne k nej sa vytvorí ustálená koncentrácia otravných produktov. Ak teraz výkon reaktora klesne na veľmi malú hodnotu až nulovú, bude v prvopočiatku koncentrácia  rásť, až dosiahne maximálnu hodnotu a potom prirodzeným rozpadom sa jeho koncentrácia zmenší.

13.2.1 Hromadenie 135I

Analyticky teraz vyšetríme zmenu koncentrácie . Pretože polčas premeny  je 2 minúty, budeme predpokladať, že  vzniká priamo ako produkt štiepenia  s výťažnosťou = 0,056. Jeho rozpadová konštanta je rovná = 2,9239.10-5 s-1. Mikroskopický účinný prierez absorpcie tepelných neutrónov je zanedbateľne malý. Koncentráciu  označíme NI. Potom rýchlosť zmeny koncentrácie  je daná súčtom vznikajúcich a zanikajúcich jadier  v jednotke objemu každú sekundu, môžeme teda písať:

                                                      (13.30)

Pretože  je veľmi malé, môžeme druhý sčítanec na pravej strane (13.30) zanedbať, potom pre rýchlosť zmeny koncentrácie jadier jódu platí:

                                                                    (13.31)

Koncentrácia  sa s časom bude zvyšovať, až dosiahne rovnovážny stav, kedy sa rýchlosť vzniku jadier uvedeného izotopu jódu zo štiepenia rovná rýchlosti ich zániku rádioaktívnym rozpadom. Pri ustálenej výkonovej úrovni zodpovedajúcej ustálenej hustote toku tepelných neutrónov sa postupne rýchlosť zmeny koncentrácie  znižuje, až dosiahne nulovú hodnotu , potom platí:

                                                                                   (13:32)

Z posledného vzťahu vyjadríme rovnovážnu koncentráciu jódu :

                                                                                 (13.33)

Riešme teraz diferenciálnu rovnicu (13.31), preto ju vynásobme integračným činiteľom . Po úprave obdržíme:

                                          (13.34)

Úpravou ľavej strany obdržíme:

                                                              (13.35)

Takto upravenú diferenciálnu rovnicu riešime integráciou v medziach od 0 až t:

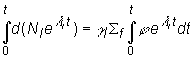                                                         (13.36)

Obecne môže byť hustota toku neutrónov funkciou času , jej vyjadrenie potom dosadíme a urobíme integráciu. V reálnej praxi však reaktor pracuje dlhodobo na ustálenej výkonovej úrovni, tj. hustota toku neutrónov sa s časom nemení. Potom po integrácii platí:

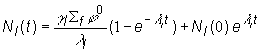                                         (13.37)

kde        je počiatočná koncentrácia . Po výmene paliva, keď bol reaktor odstavený dlhú dobu, bude počiatočná koncentrácia  rovná nule. Naopak po náhlej zmene výkonu reaktora dlhú dobu pracujúceho na ustálenom výkone, bude počiatočná koncentrácia  rovná ustálenej koncentrácii pred zmenou atď.

Ak je napríklad výkon reaktora náhle znížený v t = 0, bude  a pre koncentráciu  môžeme zapísať:

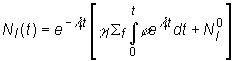                                                           (13.38)

Vzťah (13.37) obsahuje člen , ktorý svoju hodnotu s rastúcim časom od spustenia reaktora, alebo zmeny výkonu, postupne zväčšuje až dosiahne hodnotu 1. Teoreticky túto hodnotu dosiahne až pri t=, prakticky sa jeho hodnota už podstatne nemení od  . Preto koncentráciu NI považujeme za ustálenú, ak od zmeny výkonu, či spustenia reaktora uplynulo aspoň päť polčasov premeny 135I.

13.2.2 Hromadenie 135Xe

Koncentráciu jadier  označíme NXe. Rýchlosť zmeny koncentrácie jadier  vyjadríme ako súčet jadier  vznikajúcich rozpadom  a štiepením jadier paliva zmenšený o množstvo zanikajúcich jadier  rádioaktívnym rozpadom a vyháraním v jednotke objemu každú sekundu. Pre rýchlosť zmeny koncentrácie  môžeme teda písať :

                      (13.39)

Pri ustálenej výkonovej úrovni dosiahne po čase koncentrácia  v reaktore rovnovážny stav, t.j. . Keďže  sa rozpadá rýchlejšie ako , čo vyjadruje vzťah medzi ich rozpadovými konštantami, >, respektívne polčasmi rozpadu <, bude aj koncentrácia  ustálená. Obdobne ako v predošlom, aj 135Xe dosiahne ustálenú koncentráciu, ak od výkonovej zmeny alebo spustenia reaktora uplynie aspoň päť polčasov jeho premeny, tj. aspoň po 46 hodinách. Takže pre ustálený stav platí:

                                      (13.40)

Pre ustálenú koncentráciu  potom platí:

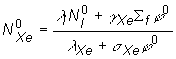                                                              (13.41)

Do (13.41) dosadíme za ustálenú koncentráciu  zo vzťahu (13.33),úpravou obdržíme pre ustálenú koncentráciu :

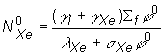                                                                 (13.42)

Diferenciálnu rovnicu (13.39) vynásobíme integračným činiteľom v tvare , úpravou obdržíme:

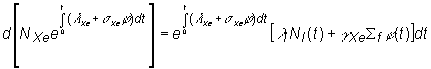          (13.43)

Koncentráciu  obdržíme, ak vzťah (13.43) integrujeme, takto po úprave platí:

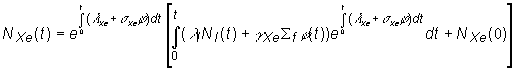            (13.44)

Pri odvodení vzťahu (13.44) sme vychádzali z predpokladu, že hustota toku neutrónov j je počas prevádzky reaktora nemenná. Po spustení reaktora s čerstvo zavezeným palivom alebo dlhodobej odstávke sa koncentrácia jadier  bude postupne zvyšovať, prirodzene sa bude zvyšovať aj koncentrácia . Dosaďme vzťah 13.43 pre koncentráciu  do (13:37), aby sme obdržali konečný vzťah pre koncentráciu jadier :

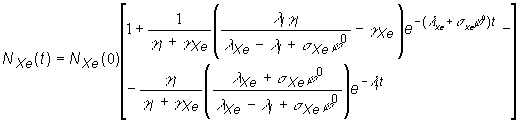(13.45)

Otravu reaktora qXe definujeme ako pomer počtu tepelných neutrónov absorbovaných otravnými produktmi štiepenia k počtu tepelných neutrónov, ktoré sú pohltené palivom v jednotke objemu za jednu sekundu. Hustotu absorpcie neutrónov v otravných produktoch štiepenia vyjadríme ako súčin . Hustota absorpcie v palive je rovná súčinu . Potom podľa definície pre otravu platí:

                                                       (13.46)

Otrava spôsobená  v ustálenom stave je daná:

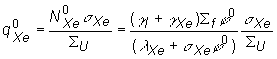                                     (13.47)

Obdobne by sme obdržali výraz pre otravu qXe(t), ak do (13.46) dosadíme (13.45).

13.2.3 Vplyv otravy na reaktivitu sústavy.

Vplyv otravy sa na reaktivite prejaví v zmene keff. Postupne analyzujme vplyv otravných produktov štiepenia na efektívny multiplikačný koeficient , ktorý je vyjadrený vzťahom:

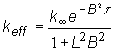
Pod vplyvom zvýšenej absorpcie spôsobenej otravnými produktmi štiepenia v AZ sa zmenší kvadrát difúznej dĺžky L2. Nakoľko koncentrácia otravných produktov je malá, nevplýva na zmenu , preto únik spomaľujúcich sa neutrónov zo sústavy sa nemení. Množivé vlastnosti štiepneho prostredia vyjadrené multiplikačným koeficientom pre nekonečné prostredie  sa menia, lebo sa zníži podiel neutrónov absorbovaných v palive, čo vyjadruje koeficient tepelného využitia f.

Keďže energetické reaktory majú hodnotu úniku tepelných neutrónov len málo líšiacu sa od nuly, bude vplyv otravy na tento únik slabo pozorovateľný.

Jediné čo vplýva podstatne na zmenu keff je zmena koeficienta tepelného využitia f. Nech koeficient tepelného využitia bez prítomnosti otravy je rovný:

                                                                         (13.48)

kde     ,,  je makroskopický účinný prierez absorpcie neutrónov v palive, moderátore a konštrukčných častiach AZ. Ak posledný vzťah upravíme tak, že čitateľa aj menovateľa podelíme , obdržíme:

                                                                              (13.49)

kde     qM a qK           vyjadrujú pomernú absorpciu v moderátore a konštrukčných častiach AZ

Koeficient tepelného využitia štiepneho prostredia s otravnými produktmi štiepenia je rovný:

                                                             (13.50)

Obdobne upravíme aj (13.50) tým, že čitateľa aj menovateľa delíme ,potom platí:

                                                                 (13.51)

kde     qXe      je otrava

Pre obrátenú hodnotu (13.51) platí:

                                                                                    (13.52)

Zmenu reaktivity reaktora spôsobenú prítomnosťou otravných produktov vyjadríme pomocou definičného vzťahu pre reaktivitu:

                                                                        (13.53)

kde         je efektívny multiplikačný koeficient reaktora s otravnými produktmi štiepenia

Na začiatku tejto kapitoly sme konštatovali, že otravné produkty vplývajú na keff prostredníctvom koeficienta tepelného využitia, preto zmenu reaktivity spôsobenú otravou môžeme vyjadriť:

                                                                     (13.54)

Ak dosadíme do posledného vzťahu (13.52), obdržíme:

                                                                                (13.55)

Zo vzťahu (13.55) vyplýva , že reaktivita viazaná otravou  je priamoúmerná súčinu koeficienta tepelného využitia a otravy qXe. To, že otravnými produktmi je reaktivita viazaná, vyjadruje na ľavej strane rovnice znamienko mínus. Stacionárna Xe-vá otrava činí u reaktorov VVER = 2,45%.


 


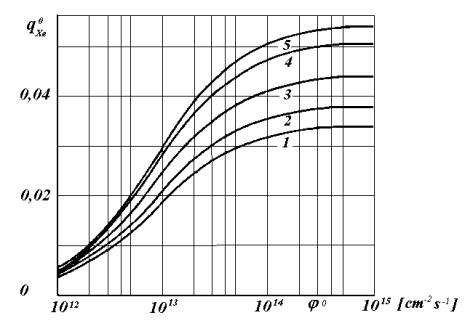
Obr.13.2. Závislosť stacionárnej otravy od ustálenej hustoty toku neutrónov.

13.2.4 Nestacionárna xenónová otrava

V aktívnej zóne jadrového reaktora vzniká približne 95% jadier 135Xe rádioaktívnym  rozpadom 135I, ktorý má polčas rozpadu 6,7 h. Bezprostredne po odstavení reaktora, ale aj po znížení jeho výkonu, je koncentrácia jadier 135I rovná ustálenej hodnote. Pokračuje tvorba 135Xe s klesajúcou intenzitou s polčasom 6,7h. Súčasne sa podstatne zníži úbytok jadier 135Xe účinkom absorpcie neutrónov. Po odstavení alebo znížení výkonu reaktora sa bude koncentrácia 135Xe zvyšovať, pretože polčas rozpadu 135Xe (9,1h) je väčší ako polčas rozpadu 135I. V odstavenom reaktore 135I nevzniká, alebo pri zníženom výkone vzniká s menšou intenzitou, takže koncentrácia 135Xe prechádza maximom a potom postupne klesá. Pomocou vzťahu (13.44) je možné určiť výraz pre zmenu koncentrácie jadier 135Xe, alebo xenónovej otravy po odstavení alebo znížení výkonu reaktora. Priebeh xenónovej otravy po náhlom odstavení reaktora, ktorý pracoval dostatočne dlhú dobu na ustálenom výkone odpovedajúcom hustote toku neutrónov , je názorný z obr.13.3. Z obrázku je zrejmé, že po odstavení reaktora (krivka 1) dosiahne otrava maximálnu hodnotu  po 10 až 12 hodinách. Veľkosť maxima silno závisí od ustálenej hodnoty hustoty toku neutrónov  pred odstavením reaktora.


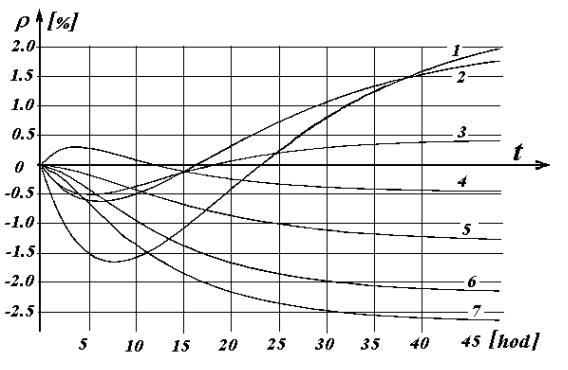
Obr.13.3. Časový priebeh xenónovej otravy po náhlom odstavení reaktora.

Na obr.13.3 sú uvedené priebehy nestacionárnej xenónovej otravy po náhlej zmene výkonu reaktora: 1- zo 100%Nnom na 0%Nnom; 2- z 50%Nnom na 0%Nnom; 3- zo 100%Nnom na 50%Nnom; 4- z 55%Nnom na 100%Nnom; 5- z 0%Nnom na 20%Nnom; 6- z %Nnom na 55%Nnom; 7- z 0%Nnom na 100%Nnom. Nárast xenónovej otravy po zníženi výkonu sa využíva pri prekonávaní prechodových efektov reaktivity v reaktore, napomáha viazať uvoľnenú reaktivitu teplotnými zmenami chladiva a paliva. V niektorých prípadoch však môže negatívne vplývať na bilanciu reaktivity po odstavení reaktora, najmä na konci kampane, keď je operatívna zásoba reaktivity už malá. Ak je operatívna zásoba reaktivity menšia, ako viazaná reaktivita otravou, reaktor nie je možné spustiť. Stav, keď reaktor nie je možné spustiť kvôli vysokej úrovni otravy, sa v reaktorovej technike nazýva iódova jama a je významný tým, že pri nevhodných manipuláciách s výkonom reaktora, spôsobuje jeho nútené odstavenie na niekoľko desiatok hodín. Ak je potrebné reaktor náhle odstaviť, nesmie byť doba odstavenia dlhšia ako 3 až 4 hodiny, inak by opätovné spustenie reaktora bolo možné až po ďalších 10 hodinách. Z tohto pohľadu je vhodné postupné alebo pomalé odstavovanie reaktora.

13.3 Zastruskovanie reaktora

Ako sme už v predošlom uviedli, pri štiepení vznikajú v aktívnej zóne reaktora ďalšie štiepne produkty s veľkým mikroskopickým účinným prierezom absorpcie tepelných neutrónov, ktoré sú buď stabilné alebo majú dlhý polčas rozpadu. V súvislosti s rastúcou koncentráciou týchto izotopov hovoríme o zastruskovaní reaktora. Zastruskovanie qstr, je definované ako pomer absorpcie neutrónov v struske k absorpcii v palive:

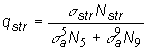                                                                                 (13.56)

kde     a N5         je mikroskopický účinný prierez absorpcie, respektívne koncentrácia 235U,

             a N9         je mikroskopický účinný prierez absorpcie neutrónov a koncentrácia 239Pu.

13.3.1 Rozdelenie strusiek do skupín

Podľa veľkosti mikroskopických účinných prierezov absorpcie tepelných neutrónov v porovnaní s absorpciou v Uráne 235U charakterizovanom , môžeme strusky rozdeliť na tri skupiny.

1; Silno absorbujúca struska  - túto skupinu tvoria izotopy: 151Sm, 149Sm, 157Gd, 155Eu a 113Cd. Táto skupina strusiek dosahuje rovnovážny stav už pri malom vyhorení paliva.

2; Priemerne absorbujúca struska  - tvoria ju izotopy: 152Eu, 152Sm, 143Nd, 131Xe, 103Rh, 99Tc a 83Kr

3; Slabo absorbujúca struska  - sem patria všetky ostatné strusky ako sú:144Nd, 139La, 133Cs a 95Mo.


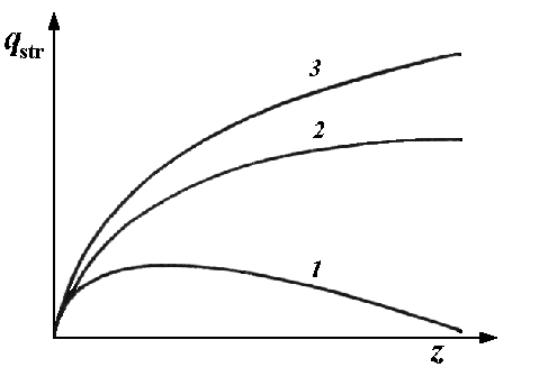
Vplyv jednotlivých skupín strusky na reaktivitu v závislosti od hĺbky vyhorenia paliva je na obr.13.4. Prvá skupina strusiek dosahuje veľmi skoro nasýtený stav, následne klesá jej množstvo v dôsledku zvyšovania hustoty toku tepelných neutrónov pri nemennom výkone reaktora. Nárast hustoty toku neutrónov je spôsobený vyháraním paliva a nutnosťou zachovania výkonu. Koncentrácia i makroskopický účinný prierez štiepenia klesá u 235U s dĺžkou prevádzky, preto musí rásť hustota toku neutrónov tak, aby výkon zostal nezmenený. Nakoniec najviac na reaktivitu vplýva najslabšie absorbujúca skupina strusiek v dôsledku vysokej koncentrácie.

Obr.13.4. Zastruskovanie reaktora v závislosti od vyhorenia paliva.

13.3.2 Hromadenie strusky

Na určenie počtu neurónov absorbovaných v struske je potrebné odvodiť vzťahy pre časový priebeh koncentrácie jednotlivých produktov štiepenia s veľkým mikroskopickým účinným prierezom absorpcie neutrónov. Pri formulácii východzích diferenciálnych rovníc zanedbáme rádioaktívny rozpad štiepnych produktov, pretože prebieha podstatne rýchlejšie ako hromadenie strusiek. Ďalej predpokladáme, že stabilné jadro i-tej strusky vzniká priamo pri štiepení 235U s výťažnosťou , alebo štiepením 239Pu s výťažnosťou . Koncentráciu jadier 235U a 239Pu označíme N5, respektívne N9. Ak zanedbáme rezonančnú absorpciu v struske, môžeme pre časovú zmenu koncentrácie i-tej strusky Ni(t) v aktívnej zóne reaktora s hustotou toku tepelných neutrónov napísať rovnicu:

                                         (13.57)

Prvý člen na pravej strane vyjadruje rýchlosť vzniku jadier i-tej strusky v jednotke objemu a druhý člen vyjadruje úbytok jadier tejto strusky záchytom neutrónov, nazývaný tiež vyháranie strusky. Riešením tejto rovnice s počiatočnou podmienkou Ni(0)=0, za predpokladu, že reaktor pracuje s konštantným merným výkonom, má tvar:

                                 (13.58)

Pre zastruskovanie i-tou struskou platí vzťah:

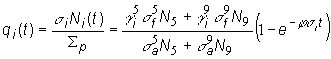                       (13.59)

Zastruskovanie a koncentrácia i-tej strusky s časom plynúcim od spustenia reaktora postupne rastú, až dosiahnu rovnovážnu alebo tiež nazývanú ustálenú hodnotu.Veľkosť ustálenej hodnoty zastruskovania závisí od použitého paliva, čo vyjadruje zlomok na pravej strane  (13.59). Doba, za ktorú dosiahne zastruskovanie ustálenú hodnotu, závisí od veľkosti mikroskopického účinného prierezu absorpcie  príslušnej skupiny strusiek ako aj od hustoty toku neutrónov. Čím bude hustota toku neutrónov väčšia, tým skôr sa pre danú skupinu strusky dosiahne ustálený stav. Ak reaktor pracuje na nominálnom výkone, ustálený stav dosiahne najskôr tá skupina strusky, ktorá má najväčší mikroskopický účinný prierez absorpcie neutrónov. Túto skutočnosť vyjadruje v (13.59) druhý člen , ktorý sa s rastúcim časom, plynúcim od spustenia reaktora, zväčšuje až dosiahne hodnotu približne rovnú jednej. Pretože výraz v zátvorke sa bude rovnať jednej, až keď sa t=, preto sa ustálená hodnota zastruskovania označuje v súlade s predchádzajúcim . Je pozoruhodné, že veľkosť ustálenej hodnoty zastruskovania nezávisí od veľkosti hustoty toku neutrónov, ale ani od veľkosti mikroskopického účinného prierezu absorpcie strusky.

Počas kampane sa v prevádzke výkon reaktora môže meniť, preto je výhodné zaviesť efektívny čas, ktorý charakterizuje stupeň vyhorenia paliva (235U) a je definovaný vzťahom:

                                                                                    (13.60)

Zastruskovanie reaktora môžeme vyjadriť pomocou efektívneho času. Ak sa hustota toku neutrónov s časom mení slabo, pre zastruskovanie platí:

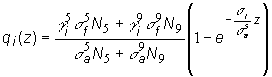                                      (13.61)

13.3.3 Vplyv zastruskovania na reaktivitu

Podobne ako pri otrave reaktora, prítomnosť strusky v aktívnej zóne vplýva na bilanciu neutrónov, mení sa efektívny multiplikačný koeficient štiepnej sústavy. Zmenu keff, podobne ako pri otravných produktoch spôsobí zmena koeficienta tepelného využitia f. Reaktivitu viazanú struskou určíme pomocou obdobného vzťahu ako pre otravu:

                                                                                    (13.62)

13.3.4 Zastruskovanie 149Sm

Pri analýze otravy a zastruskovania reaktora predstavuje, popri 135Xe, hromadenie stabilného izotopu 149Sm, ktorý má veľký mikroskopický účinný prierez absopcie tepelných neutrónov a relatívne veľký podiel vzniku pri štiepení, významný vplyv na bilanciu neutrónov. Tento izotop vzniká postupným  rozpadom izotopu neodýmu 149Nd a prometea 149Pm. Izotop neodýmu 149Nd vzniká ako priamy produkt štiepenia s výťažnosťou . Izotop  je stabilný izotop, účinný prierez pre absorpciu tepelných neutrónov = 4,01.10-20 cm2, nevzniká priamo ako produkt štiepenia , ale ako produkt rozpadu neodýmu :

 

                                                           1,73 h             53,1 h

 

Po zastavení reaktora rastie koncentrácia  podstatne pomalšie ako , pretože  má väčší polčas premeny. Účinný prierez absorpcie tepelných neutrónov je u  o dva rády menší ako u , preto je z hľadiska vplyvu na reaktivitu  menej nebezpečný. Z hľadiska vplyvu na reaktivitu reaktora ho charakterizujeme ako silne absorbujúcu strusku. Intenzita s, akou vzniká jeden alebo druhý uvedený produkt štiepenia, je úmerná výkonu reaktora.

Na rozdiel od 135Xe je 149Sm stabilný izotop a podľa jestvujúcej terminológie patrí medzi strusku. Vďaka veľkému mikroskopickému účinnému prierezu absorpcie tepelných neutrónov  pri dostatočne veľkej hustote toku tepelných neutrónov  sa počas ustálenej prevádzky reaktora vytvorí ustálená koncentrácia 149Sm ( pre VVER-440), ktoré sa prejavuje analogicky ako ustálená stacionárna otrava 135Xe ( pre VVER-440). Preto sa často (nesprávne) označuje stacionárne zastruskovanie 149Sm ako stacionárna otrava. Časovú premenlivosť koncentrácie  a zastruskovania po výkonovej zmene v reaktore spôsobuje tvorba 149Pm a zmena vyhárania . Premenlivosť reaktivity viazanej  po výkonovej zmene je ďalším dôvodom, prečo sa zastruskovanie  často označuje ako samáriova otrava.

13.3.4.1 Hromadenie 149Pm

Izotop 149Pm vzniká  rozpadom 149Nd s polčasom rozpadu 1,73 hod., je nestabilný, mení sa  rozpadom na 149Sm. Nakoľko polčas rozpadu 149Pm je podstatne väčší ako polčas rozpadu izotopu 149Nd, z ktorého vzniká, môžeme uvažovať, akoby 149Pm vznikal priamo pri štiepení s výťažnosťou .

Mikroskopický účinný prierez absorpcie tepelných neutrónov prometeom je . Koncentráciu 149Pm označíme NPm. Potom rýchlosť zmeny koncentrácie 149Pm vyjadríme nasledovne

                            (13.63)

Posledný člen vyjadrujúci vyháranie 149Pm môžeme pre malosť  zanedbať. Rovnicu (13.63) vynásobíme integračným členom  a obdržíme:

Posledný výraz integrujeme v intervale od 0 po t , potom platí:

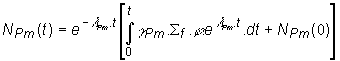                     (13.64)

kde     NPm(0)            je koncentrácia 149Pm v čase t = 0.

 Predpokladajme, že hustota toku neutrónov je konštantná (ustálená výkonová prevádzka) a označíme ju , ďalej uvažujme NPm(0) = 0, čo je pre čerstvé palivo splnené. Potom platí:

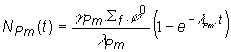                                                (13.65)

Ustálená koncentrácia 149Pm je rovná:

                                                                             (13.66)

13.3.4.2 Hromadenie 149Sm

Podobne ako v predchádzajúcom označíme koncentráciu 149Sm NSm, pre rýchlosť zmeny koncentrácie 149Sm platí bilančná rovnica:

                                             (13.67)

Poslednú rovnicu vynásobíme integračným členom , potom môžeme (13.67) zapísať v tvare:

                                   (13.68)

Do poslednej rovnice dosadíme za NPm(t) zo vzťahu (13.65) a integrujeme v intervale 0 – t, potom platí:

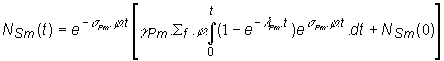       (13.69)

kde     NSm(0)            je koncentrácia 149Sm v t = 0.

Pri integrácii považujeme hustotu toku neutrónov  za časovo nemennú veličinu, ktorú označíme . Po integrácii obdržíme pre časovú zmenu koncentrácie  nasledovné:

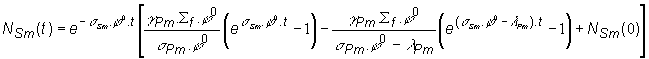(13.70)

Po úprave platí:

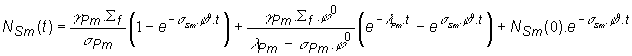(13.71)

Ustálená koncentrácia 149Sm je z (13.67) s použitím výrazu pre ustálenú koncentráciu 149Pm (13.66) rovná:

                                                                 (13.72)

Pre zastruskovanie samáriom  platí:

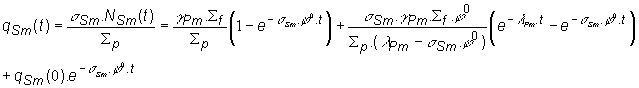(13.73)

Po dostatočne dlhom čase členy  a  nadobudnú veľmi malé hodnoty, zastruskovanie  dosiahne ustálenú hodnotu rovnú:

                                                       (13.74)

Zo vzťahu (13.74) vyplýva, že ustálená hodnota zastruskovania reaktora jadrami  nezávisí od hustoty toku neutrónov ani od absorpčných schopností jadier , závisí len od použitého paliva a výťažnosti 149Pm zo štiepenia.

Reaktivita viazaná ustálenou koncentráciou 149Sm je rovná  a pre reaktory VVER-440 sa rovná 0,6%.

Po odstavení reaktora sa koncentrácia 149Sm zvyšuje v dôsledku  rozpadu nahromadeného 149Pm. V čase t = 0 sa . Potom pre zmenu koncentrácie 149Sm platí:

                                                (13.75)

Predpokladajme, že v čase t = 0, boli koncentrácie 149Sm a 149Pm ustálené  a . Integráciu poslednej rovnice urobíme v intervale 0 až t, potom platí:

                         (13.76)

Úpravou obdržíme pre časovú zmenu koncentrácie  po odstavení reaktora nasledovný vzťah:

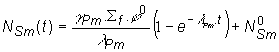             (13.77)

Pre zastruskovanie  po odstavení reaktora platí:

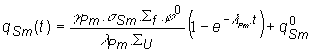     (13.78)


Po 14-tich dňoch sa v odstavenom reaktore zvýši koncentrácia  na maximálnu hodnotu, čomu zodpovedá zvýšenie viazanej reaktivity. Priebeh reaktivity viazanej zastruskovaním reaktora  po výkonovej zmene je na obr.13.5 U reaktorov VVER-440 to činí 0,3% reaktivity.

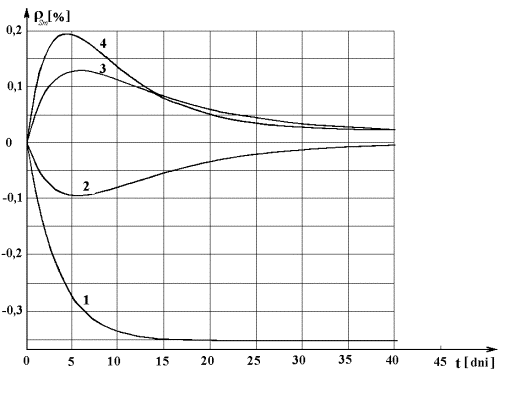
Obr.13.5 Zmena reaktivity viazanej zastruskovaním  po výkonovej zmene.

Na obr.13.5 sú priebehy viazanej reaktivity rSm v tlakovodnom reaktore, v závislosti od času, ktorý uplynul od výkonovej zmeny: 1 - z N1=100%Nnom na N2=0; 2 - z N1=100%Nnom na N2=55%Nnom; 3 - z N1=0 na N2=55%Nnom; 4 - z N1=0 na N2=100%Nnom. Pred výkonovou zmenou bola koncentrácia 149Sm ustálená, tj pred znížením výkonu reaktor pracoval na Nnom aspoň 40 dní, respektívne pred spustením bol reaktor aspoň 15 dní odstavený.

13.4 Zmeny izotopického zloženia paliva

Počas prevádzky jadrového reaktora dochádza k zmenám izotopického zloženia paliva. Znalosť izotopického zloženia paliva obsiahnutého v reaktore má spolu s

 koncentráciou strusiek podstatný význam pre prevádzku reaktora. Určuje jeho jadrové vlastnosti, rozloženie hustoty toku neutrónov, rozložení výkonovej hustoty, dynamické vlastnosti a pod. Po radiačnom záchyte neutrónu jadrom 235U sú zmeny izotopického zloženia paliva určené jadrovými procesmi uvedenými na obr.13.6.


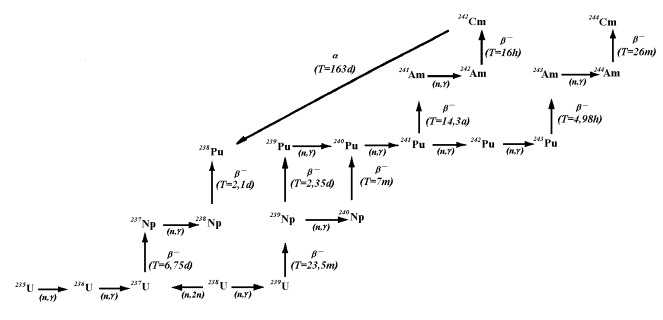
Obr.13.6 Jadrové procesy v uránovej náplni reaktora.

Nakoľko 236U a 242Pu majú malý mikroskopický účinný prierez absorpcie neutrónov, preto vznik ďalších izotopov uvedených na obr.13.6 je málo pravdepodobný. Jadrá 239U a 239Np majú relatívne malý polčas rozpadu, preto ich vplyv na dlhodobé zmeny izotopického zloženia paliva je zanedbateľný. Polčas rozpadu izotopov 235U, 238U, 239Pu, 240Pu a 241Pu je veľmi veľký, preto vplyv ich rádioaktívneho rozpadu na izotopické zloženie môžeme zanedbať.

Nakoľko rovnice popisujúce časovú zmenu koncentrácie jednotlivých izotopov paliva popisujú pomalé zmeny v reaktore, preto túto časť nazývame tiež dlhodobou kinetikou reaktora. Pri formulácii týchto rovníc, budeme koncentráciu 238U v reaktore považovať za časovo nemennú. Rezonančný záchyt neutrónov budeme uvažovať iba na jadrách 238U, pretože pri nízkej koncentrácii ostatných izotopov v reaktore bude ich rezonančný záchyt zanedbateľne malý. Veličiny vzťahujúce sa na rôzne izotopy budeme označovať indexom poslednou číslicou označujúcej hmotnostné číslo daného izotopu, tj. 235U - 5; 238U - 8; 239Pu - 9; 240Pu; - 0; 241Pu - 1 a 242Pu - 2. Mikroskopické účinné prierezy pre jednotlivé izotopy označujeme: absorpčný - , štiepenia - , radiačného záchytu - .

13.4.1 Zmena koncentrácie 235U

Bilančná rovnica popisujúca rýchlosť zmeny koncentrácie jadier 235U v palive má nasledovný tvar:

                                                                  (13.79)

Riešením tejto diferenciálnej rovnice za predpokladu, že hustota toku neutrónov je počas prevádzky nemenná, obdržíme výraz pre časovú zmenu koncentrácie jadier 235U v nasledovnom tvare:

                                                          (13.80)

Ak použijeme efektívny čas podla (13.70), ktorý uľahčí výpočet pri premenlivom výkone reaktora, obdržíme:

                                                               (13.81)

Z (13.80) vyplýva, že koncentrácia jadier 235U sa od počiatočného stavu  exponenciálne znižuje. Rýchlosť poklesu koncentrácie závisí iba od hustoty toku neutrónov, respektívne od výkonu reaktora.

13.4.2 Tvorba transuranov

Zapíšeme postupne bilančné rovnice pre jednotlivé trasuranové izotopy v palive. Budeme predpokladať, že hustota toku neutrónov sa počas prevádzky nemení, alebo jej zmena je zanedbateľne malá.

Prvý s transuranových izotopov vznikajúci počas prevádzky v reaktore je 239Pu. Vzniká záchytom tepelných a rezonančných neutrónov jadrami 238U s následným dvojnásobným rozpadom a zaniká záchytom  tepelných neutrónov, tj. platí:

                      (13.82)

kde     e          je multiplikačný koeficient rýchlych neutrónov

            p          je pravdepodobnosť úniku rezonančnému záchytu

Druhý sčítanec na pravej strane udáva v zátvorke počet rýchlych neutrónov vznikajúcich štiepením 235U a 239Pu pohltených počas spomaľovania v rezonančnej oblasti v 238U.Pravdepodobnosť, že neutrón bude pohltený v rezonančnej oblasti jadrami 238U, vyjadruje člen (1-p).

Druhý z transuranov je izotop 240Pu, ktorý vzniká radiačným záchytom tepelných neutrónov jadrami 239Pu a zaniká záchytom tepelných aj rezonančných neutrónov. Poznamenávame, že rezonančný záchyt sa na bilancii prejaví len pri hlbokom vyhorení paliva, respektívne pri jeho dostatočne vysokej koncentrácii. Pre rýchlosť zmeny koncentrácie jadier 240Pu platí:

                                                (13.83)

Izotop 240Pu nie je štiepitelný tepelnými neutrónmi, je ho možné štiepiť len neutrónmi s energiou väčšou ako 1MeV.

Záchytom na jadrách 240Pu vzniká ďalší izotop plutónia 241Pu, ktorý zaniká záchytom neutrónov. Tento izotop je štiepitelný neutrónmi všetkých energií. Rýchlosť zmeny koncentrácie 241Pu má tvar:

                                                     (13.84)

Posledný nami uvažovaný izotop plutónia 242Pu vzniká radiačným záchytom neutrónov jadrami 241Pu a zaniká záchytom tepelných neutrónov, pre rýchlosť zmeny koncentrácie platí:

                                         (13.85)

Ako už bolo uvedené, keď je koncentrácia jadier 240Pu dostatočne vysoká neplatí bilančná rovnica (13.80). V tomto prípade už musíme uvážiť aj rezonančný záchyt spomaľujúcich sa neutrónov jadrami 240Pu. Rýchlosť zmeny koncentrácie 240Pu má potom nasledovný tvar:

   (13.86)

Posledná rovnica je však nelineárna, pretože pravdepodobnosť , že sa neutrón vyhne rezonančnému záchytu v 240Pu pri spomaľovaní, závisí od koncentrácie tohto izotopu. V tomto prípade systém diferenciálnych rovníc (13.79) až (13.86) musíme

 riešiť numericky. Časová zmena koncentrácie jednotlivých izotopov je názorná z obr.13.7.


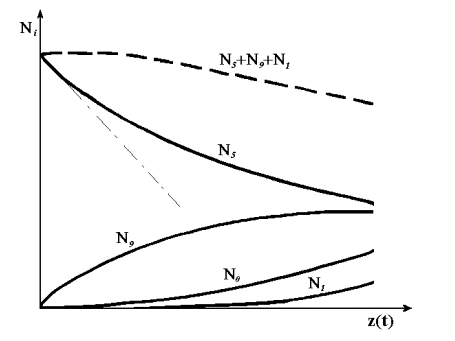
Obr.13.7 Časový priebeh koncentrácie izotopov v palive

13.4.3 Vplyv zmien izotopického zloženia na vlastnosti reaktora

Zmena izotopického zloženia paliva má vplyv na efektívny multiplikačný koeficient prevádzkovaného reaktora. Meniaci sa obsah štiepnych izotopov v palive má bezprostredný vplyv na regeneračný koeficient h a koeficient tepelného využitia paliva f. Regeneračný koeficient, ktorý vyjadruje priemerný počet neutrónov vznikajúcich pri záchyte neutrónu, môžeme vyjadriť vzťahom:

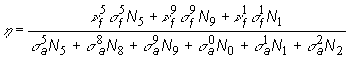                   (13.87)

Koncentrácia jadier izotopu 238U sa nemení s časom, podstatný vplyv na zmenu regeneračného koeficienta má pokles koncentrácie jadier 235U a rast koncentrácie 239Pu. Na počiatku prevádzky reaktora môže h mierne rásť, ale postupne sa prejaví výraznejší pokles koncentrácie jadier 235U, čo spôsobí aj jeho pokles.

Druhou veličinou, ktorá sa počas prevádzky reaktora mení, je koeficient tepelného využitia paliva f, ktorý môžeme vyjadriť nasledovne:

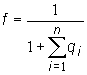                                                                        (13.88)

Pomerná absorpcia qi obsahuje podľa definície v čitateli neutróny absorbované v i-tom izotope, v menovateli je počet absorbovaných neutrónov v palive. Nakoľko sa koncentrácia jednotlivých izotopov v palive s časom mení, budú pomerná absorpcia a koeficient tepelného využitia paliva závislé od času. Počas prevádzky reaktora monotónne klesá hodnota koeficienta tepelného využitia paliva.

13.4.3.1 Konverzia paliva

Záchytom neutrónov jadrami 238U vzniká nový veľmi kvalitný štiepny materiál plutónium 239Pu. Tvorba izotopu 239Pu ma veľký význam z hľadiska zvýšenia energetickej výťažnosti paliva tepelných reaktorov bezprostredne v reaktore ako aj možnosti reprodukcie paliva s využitím prepracovacích závodov. Veličina, ktorá nám umožňuje hodnotenie tvorby nového štiepneho materiálu, je konverzný faktor CR (Convesion Ratio), ktorý je definovaný ako pomer počtu jadier novovznikajúceho paliva k počtu vyhorených (spotrebovaných) jadier pôvodného paliva. V tepelných reaktoroch pracujúcich na prírodnom alebo slabo obohatenom uráne je konverzný faktor určený vzťahom:

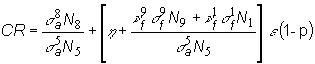               (13.89)

S rastom obohatenia paliva klesá konverzný faktor. U tepelných reaktorov je konverzný faktor menší ako jedna, tj. spotrebujeme viac paliva, ako vyrobíme nového. Najväčšiu hodnotu má CR u ťažkovodných reaktorov, kde sa pohybuje okolo hodnoty 0,9 , v tlakovodných reaktoroch je hodnota konverzného faktora menšia ako 0,6.Rýchle reaktory umožňujú rozšírenú reprodukciu paliva v blanketnej zóne obklopujúcej aktívnu zónu s vysoko obohateným palivom. Tu hovoríme o množení paliva a veličina vyjadrujúca vznik nového paliva, sa nazýva množivý faktor BR (Breeding Ratio). Množivý faktor je rovnako definovaný ako konverzný faktor, rozdiel je len v tom, že BR môže byť väčšie ako jedna.

13.4.3.3 Zmena efektívneho podielu oneskorených neutrónov

Zmena izotopického zloženia paliva počas prevádzky reaktora sa prejaví aj na efektívnom podiele oneskorených neutrónov. Počas kampane je zmena  spôsobená hlavne klesajúcim počtom štiepení jadier 235U s podielom oneskorených neutrónov , spôsobeného poklesom koncentrácie a nárastom počtu štiepení jadier 239Pu s nižším podielom oneskorených neutrónov , vyvolaného rastom jeho koncentrácie. Z uvedeného vyplýva, že efektívny podiel oneskorených neutrónov počas prevádzky reaktora s uránovým palivom postupne klesá. Pokles efektívneho podielu oneskorených neutrónov sa prejaví na dynamických vlastnostiach štiepneho systému, veľkosť zmien reaktivity v reaktore musí zohľadňovať túto skutočnosť. Napríklad v prvýkrát spustenom reaktore s uránovým palivom je na počiatku efektívny podiel oneskorených neutrónov , ktorý postupom vyhárania klesne ku koncu kampane na .

Pokúsime sa teraz určiť podiel oneskorených neutrónov vznikajúcich pri štiepení v prostredí tvorenom zmesou izotopov paliva. Podiel oneskorených neutrónov je určený pomerom počtu vznikajúcich oneskorených neutrónov k počtu všetkých neutrónov vznikajúcich pri štiepení. Počet neutrónov vznikajúcich pri štiepení môžeme určiť ako súčin rýchlosti štiepenia a priemerného počtu neutrónov vznikajúcich pri jednom štiepení, tj . Počet oneskorených neutrónov bude potom úmerný počtu neutrónov vznikajúcich pri štiepení, čo môžeme zapísať ako .

Ak štiepne prostredie obsahuje zmes izotopov paliva, potom na základe prechádzajúcej úvahy môžeme určiť podiel oneskorených neutrónov nasledovne:

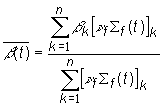                                                     (13.90)

kde     k          je index označujúci štiepny izotop,

                  je celkový podiel oneskorených neutrónov vznikajúcich pri štiepení k-tého izotopu.

Podobne môžeme určiť efektívny podiel oneskorených neutrónov v štiepnom prostredí tvorenom zmesou izotopov paliva:

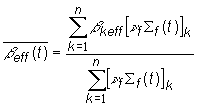                                                         (13.91)

V predchádzajúcom sme neuvažovali množstvo oneskorených neutrónov vznikajúcich pri štiepení 238U rýchlymi neutrónmi, ak ich podiel uvážime, potom výraz pre efektívny podiel oneskorených neutrónov bude mať tvar:

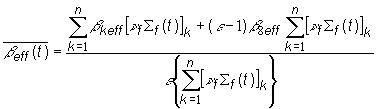                       (13.92)

kde       je efektívny podiel oneskorených neutrónov vznikajúcich pri štiepení 238U, pričom podiel oneskorených neutrónov b8=0,0158

e                    je multiplikačný koeficient rozmnoženia na rýchlych neutrónoch

Množstvo oneskorených neutrónov vznikajúcich pri štiepení jadier 238U vyjadruje druhý sčítanec v čitateli (13.92).