10. Heterogénny reaktor

Prakticky všetky reaktory sú heterogénne.V heterogenných reaktoroch je spomaľovanie  neutrónov priestorovo oddelené od ich absorpcie. Neutróny strácajú svoju energiu v moderátore, a pohlcované sú v palive, čo spôsobuje rôznosť hustoty toku neutrónov v rozličných zložkách aktívnej zóny reaktora.Vplyv rozloženia hustoty toku neutrónov v elementárnej bunke na množivé vlastnosti štiepneho prostredia (takzvaná fyzikálna heterogénnosť),závisia od energie neutrónov. Reaktor je fyzikálne heterogénny pre neutróny jednej oblasti energie (napríklad tepelnej ),môže však byť prakticky homogénny pre neutróny inej oblasti energie (napr. pre neutróny vznikajúce štiepením s E0=1MeV).Priebeh hustoty toku neutrónov s rôznymi energiami v elementárnej bunke je na obr.10.2 a 10.4.Rozbor reťazovej reakcie štiepenia v tepelnom reaktore pozostáva z dvoch častí :


mikroskopickej teórie a makroskopickej teórie. Doposiaľ sme sa zaoberali makroskopickou teóriou reaktora, ktorá zahrňuje výpočet kritickej veľkosti reaktora, priestorové rozloženie hustoty toku neutrónov, atď. Mikroskopická teória reaktora sa zaoberá výpočtom multiplikačného koeficientu v nekonečnom prostredí . Tento koeficient je dôležitou vnútornou charakteristikou množivej sústavy. Je závislý od počtu okamžitých neutrónov, ktoré vznikajú na jeden zachytený tepelný neutrón v , od veľkosti makroskopických účinných prierezov absorpcie a rozptylu. Je taktiež závislý od tvaru a rozmerov reaktorovej mriežky, alebo elementárnej bunky.

 


Obr.10.1 Heterogénne usporiadanie paliva a moderátora.

Tieto vlastnosti nazývame mikroskopickými, pretože nezávisia od celkových rozmerov sústavy.V reaktoroch na prírodnom alebo slabo obohatenom uráne nastávajú štyri rôzne, navzájom si konkurujúce spôsoby absorpcie :

a) absorpcia rýchlych neutrónov s energiou väčšou ako je prah štiepenia .

b) radiačné zachytenie neutrónov jadrami  v rezonančnej oblasti.

c) radiačné zachytenie tepelných neutrónov v materiáloch AZ, t.j. v moderátore, konštrukčných materiáloch, atď.

d) pohltenie tepelných neutrónov jadrami , ktoré spôsobuje ich štiepenie.

Určiť multiplikačný koeficient znamená, určiť relatívny pomer medzi jednotlivými druhmi pohtenia neutrónov v aktívnej zóne.

Ako sme  už viackrát uviedli, s klesajúcou energiou neutrónov rastie mikroskopický účinný prierez absorpcie v jednotlivých materiáloch AZ. V štiepnej sústave na prirodzenom alebo nízko obohatenom uráne je najviac ťažkých izotopov  . Tento izotop štiepia iba neutróny, ktorých energia je väčšia ako 1,1 MeV. Neutróny nižších energií sú  zachytávané bez možnosti štiepenia týchto jadier. Platí tu taktiež, že mikroskopický účinný prierez absorpcie  rastie s klesaním energie neutrónov, až v tepelnej oblasti dosiahne hodnotu 2,8.10-24 cm2. V rezonančnej oblasti však mikroskopický účinný prierez,  nadobúda značne väčšie  hodnoty. Podstatnú úlohu, pre prácu reaktora, má absorpcia neutrónov v . Tohto izotopu, čo do percentuálneho zastúpenia, je v AZ podstatne menej než , ale jeho  s klesaním energie neutrónov rastie a v tepelnej oblasti nadobúda hodnotu približne  a jeho . Takto viac ako polovica neutrónov absorbovaných v AZ pripadá na absorpciu v . Preto je výhodné neutróny spomaľovať na tepelné. Ako moderátor budeme vyberať taký materiál, ktorého koeficient spomaľovania  je čo najväčší. Na materiál moderátora sú kladené i ďalšie požiadavky, ako sú cena za jednotku objemu, dostupnosť od výrobcu, možnosť stáleho spracovania počas prevádzky jadrového reaktora ( čistenie od koróznych produktov ), atď.

 

10.1 Regeneračný súčiniteľ

Prvým zo súčiniteľov, ktorý vystupuje v multiplikačnom koeficiente, je počet rýchlych neutrónov vznikajúcich na jeden zachytený tepelný neutrón. Označujeme ho „“.

 

                                                                            (10.1)

 

kde - je priemerný počet okamžitých neutrónov štiepenia pripadajúcich na jeden akt štiepenia, pre  sa .

- mikroskopický účinný prierez štiepenia

- mikroskopický účinný prierez absorpcie

Podiel mikroskopických účinných prierezov  vyjadruje pravdepodobnosť štiepenia pri záchyte tepelného neutrónu.Obdobne pomer  predstavuje pravdepodobnosť radiačného zachytenia.Ak tento pomer označime , potom platí:

                                                     (10.2)

Pre regeneračný súčiniteľ potom platí:

                                                                                   (10.3)

Pri výpočte počtu okamžitých neutrónov štiepenia na jeden zachytený tepelný neutrón môžeme miesto mikroskopických použiť makroskopické účinné prierezy, ktoré pri výpočte  obyčajne už máme určené. Potom môžeme zapísať:

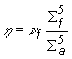                                                                                        (10.4)

 

kde  a  sú makroskopické účinné prierezy štiepenia resp. absorpcie pre .

Pre zmes štiepnych materiálov  alebo iných štiepnych izotopov, v prípade ak je hustota toku tepelných neutrónov v prostredí nemenná tj. , môžeme regeneračný súčiniteľ určiť:

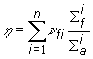                                                                                              (10.5)

Alebo ak sa hustota toku neutrónov v štiepnom prostredí mení tj. , určíme regeneračný súčiniteľ nasledovne:

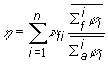                                                                               (10.6)

10.2 Multiplikačný koeficient rýchlych neutrónov

Rýchle neutróny s energiou vyššou ako 1,1 MeV môžu spôsobiť štiepenie jadier , preto ku každému rýchlemu neutrónu, ktorý vznikol pri štiepení  pomalými neutrónmi, je potrebné pripočítať istý podiel rýchlych neutrónov, ktoré vznikli štiepením . Každý rýchly neutrón má určitú pravdepodobnosť, že vyvolá štiepenie, pri ktorom vzniknú ďalšie neutróny. Multiplikačný koeficient rýchlých neutrónov  je definovaný ako priemerný počet neutrónov, ktoré sa spomalia pod energiu prahu štiepenia , pripadajúcich na jeden rýchly neutrón, ktorý vznikol pri štiepení  tepelnými neutrónmi. Pri výpočte  musíme zahrnúť všetky rýchle neutróny, ktoré vznikajú v kaskádnom procese.

Rýchle neutróny, ktoré vznikajú v uránovom bloku, sa spomaľujú dvoma spôsobmi:

1) Spomalenie spôsobené nepružnými zrážkami rýchlych neutrónov s jadrami . Pri nepružných zrážkach hodnota energie neutrónu prudko klesne na energiu podstatne nižšiu ako je prah štiepenia .

2) Neutróny sú spomaľované po úniku z palivového článku moderátorom. Môžeme s dostatočnou presnosťou počítať, že rýchle neutróny, ktoré prenikli do moderátora, sa do palivového bloku nevrátia s energiou vyššou ako prah štiepenia .

3) Pružné rozptylové zrážky rýchlých neutrónov s ťažkými jadrami nespôsobujú pozorovateľné zmeny ich energie, preto v ďalšom budeme predpokladať, že neutróny pružnými zrážkami v palivovom článku svoju energiu nestrácajú.

Nech je P pravdepodobnosť, že sa rýchly neutrón vzniknutý pri štiepení zrazí s palivom v bloku.

Potom pre jeden rýchly neutrón môžeme písať :

Počet zrážok v bloku                                                                      P

Počet rýchlých neutrónov vzniknutých po prvej zrážke   

Počet pružných zrážok                                                       

Počet neutrónov, ktoré unikli z bloku                                 1 - P

Počet neutrónov, ktoré prekonali nepružnú zrážku                     

kde ,   pre .

Rýchle neutróny, ktoré prekonali zrážku v bloku, sú rozložené rovnomerne, kým rýchle neutróny, ktoré vznikajú pri štiepení , sú rozložené úmerne hustote toku tepelných neutrónov v bloku.

Preto pravdepodobnosť druhej a nasledujúcich zrážok je väčšia ako P, označme si ju .Podobným spôsobom určime aj počet ďalších zražok neutrónov v palivovom bloku.

Úhrnný počet neutrónov spomalených pod prah štiepenia  na jeden rýchly neutrón  je dané ako súčet všetkých neutrónov spomalených pod prah štiepenia . Čo vyjadruje súčet neutrónov, ktoré unikli z palivového bloku do moderátora a neutrónov, ktoré prekonali nepružnú rozptylovú zrážku. Multiplikačný koeficient rýchlych neutrónov určime potom:

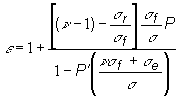                                                             (10.7)

Pri praktických výpočtoch  sa na určenie pravdepodobnotí zrážky v bloku používajú tabuľky, alebo nomogramy v ktorých sú uvedené pravdepodobnosti P a  ako funkcie súčinu . Kde - je celkový makroskopický účinný prierez  a Ru  je polomer palivového bloku - tyčky.

10.3 Pravdepodobnosť úniku rezonančnému zachyteniu

Pravdepodobnosť úniku rezonančnému zachyteniu p,  je definovaná ako počet neutrónov, ktoré dosiahli tepelnú oblasť k počtu neutrónov, ktoré začali spomaľovanie. Bez odvodzovania zapíšeme obecný výraz pre pravdepodobnosť úniku rezonančnému zachyteniu:

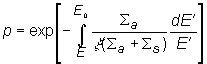                                                      (10.8)

kde E0 - je rovná 2 MeV, E - ľubovoľná energia

 a  sú makroskopické účinné prierezy pre elementárnu aktívnu bunku

- priemerný logaritmický dekrement energie

Absorpčné vlastnosti elementárnej bunky vyjadruje súčet makroskopických účinných prierezov paliva a moderátora . Je prirodzené, že moderátor v porovnaí s palivom neutróny neabsobuje tj.,, preto pod  rozumieme makroskopický účinný prierez absorpcie paliva.

Hoci výraz (10.8), platí presne len pre vodíkový moderátor a absorpčnú látku tvorenú veľmi ťažkými prvkami, je možné použiť tento výraz aj pre výpočet p pre iné moderátory. Pri výpočte pravdepodobnosti úniku rezonančnému zachytu neutrónov sa však obmedzíme na prípady, keď rezonancie absorbujúcich jadier budú od seba dostatočne ďaleko, alebo keď rezonančné zachytenie bude malé.

Ak označime počet jadier  v jednotke objemu N0, potom môžeme výraz pod integrálom vyjadriť aj:

                                              (10.9)

Účinné prierezy rozptylu  moderátora  a absorbátora v rezonančnej oblasti môžeme považovať za nezávislé od energie, preto môžeme (10.8) zapísať v tvare:

 

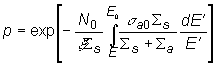                                                               (10.10)

 

V predošlom výraze sa určitý integrál nazýva efektívnym rezonančným integrálom Ieff, preto platí:

 

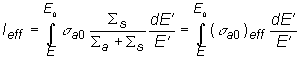                                           (10.11)

 

Kde efektívnu hodnotu mikroskopického učinného prierezu absorpcie zapíšeme v tvare:

                                                                            (10.12)

 

Takto je zrejmé, že efektívny rezonančný integrál je tiež funkciou energie, podobne ako . Potom môžeme zapísať:

 

                                                               (10.13)

 

Výraz (10.12) pre  môžeme upraviť:

 

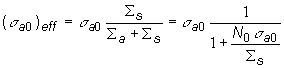                                               (10.14)

 

Veličina  je úhrnný makroskopický účinný prierez rozptylu pripadajúci na jedno jadro . Čím väčšie je N0, tým sa viac blížime k najmenšej hodnote efektívneho rezonančného integrálu, a to pre čistý . Naopak, ak sa  nachádza v nekonečne rozriedenom prostredí, kde je N0 malé, efektívny rezonančný integrál sa blíži svojej maximálnej hodnote. V tomto prípade je súčin  veľmi malý v porovnaní s jednotkou. V menovateli (10.14) môžeme preto tento súčin zanedbať. Potom platí:

 

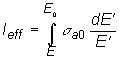                                                                            (10.15)

 

Efektívny rezonančný integrál, ako funkcia účinného prierezu rozptylu pripadajúceho na jedno jadro , bol meraný v zmesi UO2 s rôznymi rozptyľujúcimi látkami : uhlík, H2O, D2O. Zistilo sa, že efektívny rezonančný integrál nezávisí podstatne na hmotnosti rozptyľujúceho jadra a pre hodnoty  platí :

 

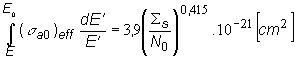                                (10.16)

 

Na výpočet Ieff sa najčastejšie používajú empirické vzťahy nasledovného tvaru :

 

                                                                  (10.17)

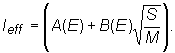                                                              (10.18)

 

Kde veličiny a(E), A(E) vyjadrujú objemovú a b(E), B(E)  povrchovú absorpciu,

S je zmočená plocha bloku uránu v elementárnej bunke  a M je hmotnosť paliva .

Podľa Wignerom experimentálne určených hodnôt sa efektívny rezonančný integrál určí pomocou vzťahu:

                                                          (10.19)

Tento výraz vyhovuje pre hrubé palivové tyče.

Pre tenké tyče používané v ľahkovodných reaktoroch sa efektívny rezonančný integrál určí pomocou vzťahu Pomerančuka-Gurieviča :

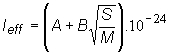                                                                (10.20)

 

Ak je známy Ieff, môžeme vypočítať pravdepodobnosť úniku rezonančnému zachyteniu v heterogénnom reaktore podľa :

 

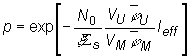                                                          (10.21)

 


Pomer  nazývame stratovým koeficientom rezonančných neutrónov. Tento pomer je menší ako jedna, pretože hustota toku rezonančných neutrónov v palive prudko poklesne následkom silnej absorpcie. Jav silnej absorpcie rezonančných neutrónov palivom sa nazýva blokovacím efektom. Blokovací efekt spôsobí zníženie absorpcie rezonančných neutrónov pri heterogénnom rozložení materiálov štiepneho prostredia v porovnaní s ich absorpciou v homogénnom prostredí.Teda v heterogénnom reaktore je väčšia hodnota pravdepodobnosti úniku rezonančnému zachyteniu neutrónov ako v homogénnom reaktore, pri použití rovnakého zloženia materiálov v AZ.

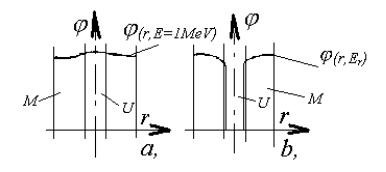
Obr.10.2 Rozloženie hustoty toku neutrónov rôznej energie v elementárnej bunke

a. rýchlych neutrónov s E=1MeV,   b. rezonančných neutrónov s Er ,

Na obr.10.2 je zrejmá rozdielnosť rozloženia hustoty toku neutrónov s energiou 1MeV a rezonančných neutrónov. V rezonančnej oblasti energií neutrónov nastáva v palive prudky pokles hostoty toku neutrónov, spôsobený veľkým účinným prierezom absorpcie jadrami . Táto skutočnosť sa prejaví znížením rezonančného záchytu neutrónov v heterogénnej zóne oproti záchytu v homogénne usporiadanom štiepnom prostredí.

 

 

10.4 Koeficient tepelného využitia.

Podľa definície, pod pojmom koeficient tepelného využitia, rozumieme pomer počtu tepelných neutrónov absorbovaných palivom  k počtu tepelných neutrónov absorbovaných v celej aktívnej zóne a označujeme ho „ f “. Pre výpočet koeficientu tepelného využitia v heterogénnej sústave použijeme niektoré zjednodušenia:

1) Predpokladáme, že hustota spomalenia v moderátore je konštantná a v palive nulová. Táto podmienka je splnená dostatočne presne, ak vzdialenosť medzi jednotlivými blokmi v mriežke nie je veľká.

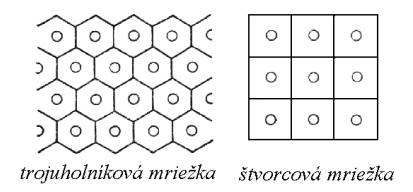
2) Heterogénnu mriežku rozdelíme na jednotlivé elementárne bunky (štvorcové, trojuholníkové) a pre výpočet uvažujeme ekvivalentnú elementárnu bunku valcového tvaru.V strede ekvivalentnej elementárnej bunky je palivový blok, jej prierez sa rovná prierezu skutočnej elementárnej bunky štvorcového alebo trojuholníkového tvaru.

3) Použijeme difúznu rovnicu, ktorá platí presne, len ak sú rozmery vyšetrovaného prostredia veľké v porovnaní so strednou voľnou dráhou rozptylu, a v mieste výpočtu niet silných stokov ani zdrojov neutrónov.


 


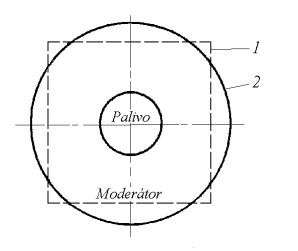
Obr.10.3 Ekvivalentná elementárne bunka 2, elementárna bunka 1..

 

Koeficient tepelného využitia v heterogénnej sústave je daný obecne:

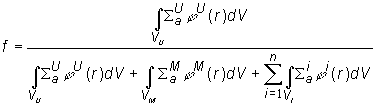                                               (10.22)

Vo vzťahu (10.22) vystupujú hustoty toku a makroskopické účinné prierezy tepelných neutrónov,použité indexy znamenajú: U – palivový blokč, M - moderátor, i - konštrukčné a prímesné materiály.

Pre zjednodušenie výpočtu budeme uvažovať elementárnu bunku, pozostávajúcu iba z paliva a moderátora. Ak zavedieme stredné hodnoty hustoty tokov tepelných neutrónov v palive a moderátore určené pomocou vzťahov:

 

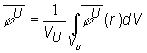                                                         (10.23)

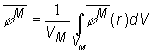                                                        (10.24)

 

Vychádzajúc z definície koeficient tepelného využitia určime pomocou vzťahu:

 

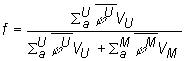                                                (10.25)

 

V homogénnom reaktore platí rovnosť objemov VU = VM ,a hutôt tokov tepelných neutrónov , preto pomernú absorpciu v palive vyjadruje pomer makroskopických účinných prierezov:

 

                                                                                   (10.26)

 

Ak zavedieme novú veličinu qM, a nazveme ju pomerným pohltením tepelných neutrónov v moderátore, bude koeficient tepelného využitia vyjadrený vzťahom:

 

                                                                                       (10.27)

kde sa pomerná absorpcia v moderátore rovná:

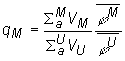                                                                           (10.28)

 


Pretože veličiny , , VU, VM sú pre určitý typ mriežky (daného zloženia) známe, redukuje sa výpočet veličiny f na určenie pomeru stredných hodnôt hustoty toku tepelných neutrónov v moderátore a palive , ktorý nazývame koeficientom nevýhodnosti rozloženia hustoty toku tepelných neutrónov v elementárnej bunke.

 


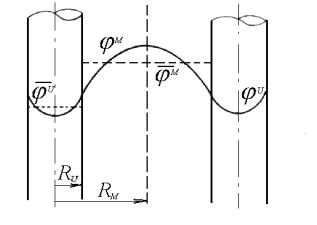
Obr.10.4 Radiálny priebeh hustoty toku tepelných neutrónov vo valcovej palivovej bunke.

Koeficient nevýhodnosti rozloženia hustoty toku tepelných neutrónov určíme riešením difúznych rovníc pre blok a moderátor za predpokladaných zjednodušení. Potom výraz pre obrátenú hodnotu koeficientu tepelného využitia bude mať tvar :

 

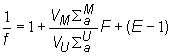                                                               (10.29)

 

 Veličina F vyjadruje pomer hustoty toku tepelných neutrónov na povrchu paliva a strednej hustoty toku tepelných neutrónov v palive tj.:

                                                                                   (10.30)

Tento pomer sa nazýva súčiniteľom samotienenia palivového bloku.

 

Nadbytočnú absorpciu v moderátore vyjadruje veličina (E - 1).

 

10.5 Makroskopická teória reaktora

V predchádzajúcom sme sa zaoberali výpočtom multiplikačného koeficientu pre nekonečnú sústavu. Určenie jednotlivých súčiniteľov , , p a f patrí do mikroskopickej teórie reaktora.Určenie kritických rozmerov aktívnej zóny a rozloženia hustoty toku neutrónov v reaktore patrí do makroskopickej teórie. Pre určenie kritických rozmerov a rozloženia hustoty toku neutrónov je potrebné poznať materiálový parameter AZ a do tohoto parametra vstupujú hodnoty ako sú difúzna dĺžka pre heterogénnu sústavu a Fermiho vek neutrónov. Preto si ich najprv stanovíme.

10.5.1 Výpočet difúznej dĺžky.

Difúzna dĺžka alebo lepšie povedané jej kvadrát je definovaný vzťahom(6.32):

 

,

 

kde D je difúzny koeficient celej AZ a  je jej absorpčný makroskopický účinný prierez.

Koeficienty difúzie pre palivo a moderátor sa od seba veľmi slabo líšia a okrem toho objem moderátora v porovnaní s objemom paliva je podstatne väčší. Preto môžeme za priemernú hodnotu koeficienta difúzie v aktívnej zóne považovať koeficient difúzie moderátora DM. Čiže D = DM. Priemernú hodnotu makroskopického účinného prierezu absorpcie pre aktívnu zónu vypočítame nasledovným spôsobom:

 

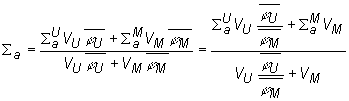                              (10.31)

Ako bolo vyššie uvedené, koeficient tepelného využitia  v heterogénnom prostredí možno určiť pomocou vzťahu (10.25) a pomocou tohto vzťahu možeme určiť absorpciu neutrónov v palive. Opäť uvedieme vyraz (10.25) a urobíme jeho postupnú úpravu:

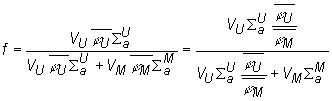                                   (10.32)

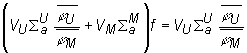                                                        (10.33)

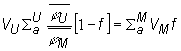                                                             (10.34)

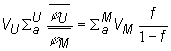                                                               (10.35)

Vzťah (10.35) dosadíme do výrazu (10.31)pre  a postupnými úpravami obdržime:

 

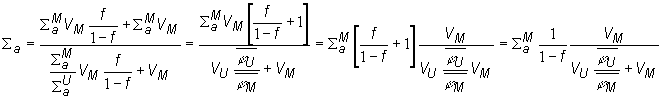
V reálnych elementárnych bunkách je objem moderátora VM ďaleko väčší ako hodnota súčinu objemu paliva a pomeru stredných hustôt toku tepelných neutrónov v palive a moderátore 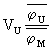, preto ju v menovateli posledného vzťahu môžeme zanedbať. Potom priemerná hodnota makroskopického účinného prierezu absorpcie pre aktívnu zónu je rovná :

                                                                                        (10.36)

Teraz, keď poznáme hodnoty priemerného koeficientu difúzie a makroskopického účinného prierezu absorpcie pre celú AZ, môžeme kvadrát difúznej dĺžky zapísať ako :

 

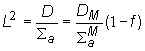                                                                      (10.37)

                                                                                 (10.38)

Pre difúznu dĺžku následne platí:

                                                                                   (10.39)

 

10.5.2 Výpočet veku tepelných neutrónov v heterogénnej sústave.

 

Spravidla sa vek neutrónov v čistom moderátore málo líši od veku neutrónov v heterogénnej mriežke, pokiaľ je objem moderátora podstatne väčší ako objem paliva v elementárnej bunke. Vek neutrónov v mriežke je o malú hodnotu väčší a to preto, že v palive nedochádza k podstatnejšiemu poklesu energie pri pružných zrážkach. Tým sa zväčšuje vek neutrónov v heterogénnom štiepnom prostredí. Je potrebné poznamenať, že v palive môžu nastať i nepružné rozptylové zrážky, ktoré naopak môžu  vek neutrónov zmenšiť.Vek neutrónov v prostredí, ktoré je tvorené zmesou látok, je podľa Galanina daný výrazom :

 

                                                          (10.40)

 

kde Ci a Cj udávajú parciálne zastúpenie i-tej a j-tej látky v zmesi a Aij sú konštanty závislé na kombinácii i-tej a j-tej látky. Hodnoty Aij pre najčastejšie používané látky v reaktorovej technike.sú tabelárne spracované.V tabuľkách sa hodnoty Aij uvádzajú pri teplote 20°C. Pretože so zmenou teploty sa mení merná hustota látky, menia sa i hodnoty Aij. Zmena mernej hustoty je pozorovateľná len u kvapalných látok, preto ju budeme uvažovať iba pri materiáloch ako sú H2O a D2O.Korekciu materiálových konštánt na teplotu prostredia určíme pomocou vťahu:

 a, pre izotopicky čistú látku

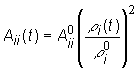                                                                       (10.41)

b, pre zmes dvoch látok

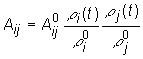                                                                      (10.42)

kde  je merná hustota i – tej látky, pri teplote t

 je hustota látky pri teplote 20 0C.

V praktických výpočtoch sa vek neutrónov pre určitý typ mriežky počíta podľa vzťahov získaných experimentálne. Napr. pre moderátor H2O a konštrukčný materiál hliník, sa vek neutrónov môže počítať podľa vzťahu:

                                                                        (10.43)

kde  a  sú objemové diely Al a paliva spolu ,respektívne H2O v elementárnej bunke.