11.
Vplyv regulačných kaziet na reaktivitu
V každom
jadrovom reaktore je potrebné mať nezávislý systém, ktorý umožňuje
podľa potreby meniť bilanciu neutrónov alebo inými slovami
regulovať štiepnu reťazovú reakciu. Vyžaduje si to vlastná prevádzka
jadrových zariadení a ich bezpečnosť. V prevádzke jadrových
zariadení je nutné zabezpečiť:
1; kompenzáciu
zásoby reaktivity, ktorá sa postupne zmenšuje v dôsledku vyhárania paliva,
2; reguláciu
výkonu vrátane spustenia a odstavenia reťazovej štiepnej reakcie ako aj
kompenzáciu malých, zato však rýchlych zmien množivých vlastností AZ vyzvaných
náhodným kolísaním parametrov reaktora, napr. kolísaním teploty chladiva,
3; rýchle
odstavenie štiepnej reťazovej reakcie v prípade, keď rozvoj
akýchkoľvek procesov v reaktore by spôsobil haváriu jadrového
zariadenia.
Základnú
časť havarijného, regulačného a kompenzačného systému (HRK)
tvoria pohyblivé absorpčné tyče alebo kazety. Riadiace tyče sú
vyhotovené z materiálu obsahujúceho prvky s vysokým účinným prierezom
absorpcie pre tepelné neutróny ![]() . V reaktoroch VVER-440 sa používajú regulačné
kazety v tandemovom usporiadaní. V hornej časti takejto kazety sa
nachádza absorbátor v podobe ocele s prídavkom karbidu bóru a
v dolnej časti sa nachádza palivo. Je potrebné poznamenať, že na
kompenzáciu zásoby reaktivity sa môžu používať vyhárajúce absorbátory.
V reaktoroch VVER-440 sa na kompenzáciu zásoby reaktivity používa roztok
kyseliny boritej v chladive. V priebehu prevádzky reaktora postupne
ubúda štiepny materiál, úmerne zmene jeho obsahu sa postupne mení aj
koncentrácia bóru v chladive. Takto sa udržuje bilancia neutrónov
v štiepnom prostredí v požadovaných medziach. V ďalšom sa budeme
venovať účinku absorpčných tyčí, respektívne kaziet na
množivé vlastnosti štiepneho prostredia. Podľa funkcie rozlišujeme
regulačné, kompenzačné a havarijné tyče. Delenie tyčí na
jednotlivé skupiny je podmienečné, v niektorých prípadoch však môže
v priebehu prevádzky prísť k ich zmene.
. V reaktoroch VVER-440 sa používajú regulačné
kazety v tandemovom usporiadaní. V hornej časti takejto kazety sa
nachádza absorbátor v podobe ocele s prídavkom karbidu bóru a
v dolnej časti sa nachádza palivo. Je potrebné poznamenať, že na
kompenzáciu zásoby reaktivity sa môžu používať vyhárajúce absorbátory.
V reaktoroch VVER-440 sa na kompenzáciu zásoby reaktivity používa roztok
kyseliny boritej v chladive. V priebehu prevádzky reaktora postupne
ubúda štiepny materiál, úmerne zmene jeho obsahu sa postupne mení aj
koncentrácia bóru v chladive. Takto sa udržuje bilancia neutrónov
v štiepnom prostredí v požadovaných medziach. V ďalšom sa budeme
venovať účinku absorpčných tyčí, respektívne kaziet na
množivé vlastnosti štiepneho prostredia. Podľa funkcie rozlišujeme
regulačné, kompenzačné a havarijné tyče. Delenie tyčí na
jednotlivé skupiny je podmienečné, v niektorých prípadoch však môže
v priebehu prevádzky prísť k ich zmene.
Vplyv
absorpčných tyčí, úplne zasunutých do aktívnej zóny reaktora, na
štiepne vlastnosti je určovaný
dvoma efektmi. Prvý vplyv na keff vyvoláva samotná absorpcia neutrónov, čo sa prejaví na bilancii
neutrónov. Druhy efekt je spôsobený zvýšením úniku neutrónov z aktívnej
zóny reaktora. Na obr.11.1 je zobrazené rozloženie hustoty toku tepelných
neutrónov v radiálnom smere v homogénnom reaktore bez reflektora pred
zasunutím (![]() ) a po zasunutí (
) a po zasunutí (![]() ) absorpčnej tyče. Po
) absorpčnej tyče. Po
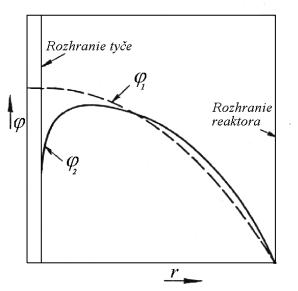
zasunutí
tyče pozorujeme určité zvýšenie hustoty toku tepelných neutrónov
v blízkosti hranice AZ, čo spôsobuje zvýšenie úniku neutrónov.
Obr.11.1
Rozloženie hustoty toku tepelných neutrónov v reaktore
s absorpčnou tyčou
Miera deformácie hustoty neutrónového toku
závisí od absorpčných schopností tyče alebo od množstva absorbovaných
neutrónov v mieste absorbátora. Je potrebne si uvedomiť, že reaktor
je v oboch prípadoch v kritickom stave a jeho výkon je rovnaký. Výkon
reaktora pred zasunutím tyče je
určený vzťahom:
![]() (11.1)
(11.1)
Výkon reaktora
po zasunutí absorpčnej tyče je obdobne rovný:
![]() (11.2)
(11.2)
kde ![]() je makroskopický
účinný prierez štiepenia
je makroskopický
účinný prierez štiepenia
![]() je energia
uvoľnená pri štiepení jedného jadra
je energia
uvoľnená pri štiepení jedného jadra
Ako
už bolo uvedené, v oboch prípadoch je výkon reaktora rovnaký, preto je
pokles hustoty toku neutrónov v okolí tyče vykompenzovaný
určitým zvýšením v miestach vzdialených od absorbátora tak, aby
hodnota objemového integrálu vo vzťahu (11.2) zostala taká istá ako pred
zasunutím tyče. Čim väčšia bude oblasť depresie hustoty
neutrónového toku v okolí tyče, tým viac sa tento zvýši
v periférnej časti AZ a opačne. Obecne možno konštatovať,
že každé zavedenie absorpčnej tyče do AZ spôsobí deformáciu
neutrónového poľa, čo spravidla zvýši nerovnomernosť výkonovej
hustoty. Preto je návrhu systému absorpčných tyčí a jeho použitiu
potrebné venovať veľkú pozornosť. Z uvedeného dôvodu sa na
kompenzáciu zásoby reaktivity používa roztok kyseliny boritej v chladive,
ktorý je homogénne rozložený po celom objeme AZ, nespôsobuje teda žiadne
deformácie neutrónového poľa. Poznamenávame, že k deformácii hustoty
toku neutrónov dochádza aj v axiálnom smere, tj. zasúvaná tyč do AZ
“vytláča” neutrónové pole k spodnej hrane reaktora.
11.1 Vplyv plne zasunutej kazety na hustotu neutrónového toku vo valcovom reaktore
Podľa účelu rozlišujeme nasledovné
absorpčné tyče:
1)
Kompenzačné tyče 2)
Regulačné tyče 3) Havarijné
tyče
Jednotlivý druh tyčí slúži na:
ad 1)
Kompenzujú prebytočnú reaktivitu AZ, ktorá je potrebná pre nepretržitú
činnosť reaktora počas kampane.
ad 2) Pomocou
týchto tyčí sa priamo reguluje štiepna reťazová reakcia udržiavaním
bilancie reaktivity rovnej nule, takto môžeme hovoriť aj o regulácii
výkonu alebo hustoty toku neutrónov v AZ. Regulačné tyče majú
malú váhu v jednotkách reaktivity, tj. ích ![]() .je malé
.je malé
ad 3) Slúžia
na rýchle zastavenie reťazovej reakcie štiepenia v AZ. Tieto tyče
majú veľkú váhu vyjadrenú v reaktivite ![]() .
.
Okrem toho, že
tieto tyče veľmi pohlcujú tepelné neutróny, deformujú rozloženie ich
hustoty toku v AZ. Ako už bolo uvedené absorpčné tyče
vytláčajú hustotu toku neutrónov do periférnej oblasti AZ, čím sa
zvýši únik neutrónov. To znamená, že riadiaca tyč vplýva na absorpčné
vlastnosti AZ, t.j. na ![]() a vplýva aj na únik
tepelných neutrónov z AZ, t.j. na
a vplýva aj na únik
tepelných neutrónov z AZ, t.j. na ![]() . V celom teda keff po zasunutí riadiacej
tyče do AZ klesá.
. V celom teda keff po zasunutí riadiacej
tyče do AZ klesá.
11.1.1 Jednoskupinová
teória regulačných tyčí.
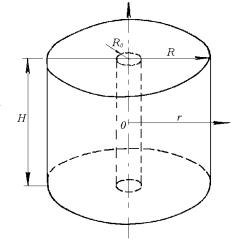
Výpočet
viazanej reaktivity ekvivalentnej jednej riadiacej tyče urobíme v
konečnej AZ valcového tvaru. Rozmery tejto AZ sú značne väčšie
ako rozmery riadiacej tyče, R0 << R, sústava je
homogénna, a bez reflektora. Riadiaca tyč je umiestnená v osi AZ.
Predpokladáme, že pri zasunutí tyče do AZ sa vytlačí z jej objemu
zodpovedajúci objem tyče. To znamená, že po vysunutí riadiacej tyče z
aktívnej zóny nezostane prázdne miesto. Tento predpoklad je pri tandemovom
usporiadaní regulačnej kazety splnený.
Obr.11.2 Valcový reaktor so zasunutou centrálnou
regulačnou tyčou.
Výpočet
vykonáme v jednoskupinovom priblížení. Kritická rovnica pre veľký, holý
reaktor v jednoskupinovom priblížení má tvar:
![]() (11.3)
(11.3)
kde ![]() je kvadrát
migračnej dĺžky
je kvadrát
migračnej dĺžky
Ak je reaktor
v kritickom stave, geometrický parameter B2 je pre valcovú aktívnu
zónu rovný súčtu:
![]() (11.4)
(11.4)
kde 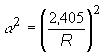 je výraz pre
únik neutrónov v radiálnom smere;
je výraz pre
únik neutrónov v radiálnom smere;
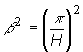 je vyraz pre únik neutrónov
v axiálnom smere;
je vyraz pre únik neutrónov
v axiálnom smere;
Potom sa
geometrický parameter rovná:
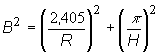 (11.5)
(11.5)
Kým je
riadiaca tyč vysunutá, má AZ tvar konečného valca o rozmeroch R a H,
pričom je započítaná už aj extrapolovaná vzdialenosť vo vákuu d.
Riešenie difúznej rovnice vyhovuje podmienkam, keď hustota toku neutrónov
je konečná a nezáporná a na extrapolovanej hranici vo vákuu klesne na
nulu.
Po zasunutí riadiacej tyče sa zmenia
okrajové podmienky. Predpokladáme, že riadiaca tyč je „ čierna “,
t.j. pohltí všetky tepelné neutróny, ktoré na ňu dopadnú. To sa dá
vyjadriť okrajovou podmienkou, keď hustota toku neutrónov klesne na
nulu v blízkosti povrchu tyče. Pričom sa polomer, na ktorom hustota
toku tepelných neutrónov klesne na nulu, rovná ![]() . Kde d - je dĺžka extrapolovanej vzdialenosti vo vákuu
a podľa transportnej teórie sa pre rovinné rozhranie rovná
. Kde d - je dĺžka extrapolovanej vzdialenosti vo vákuu
a podľa transportnej teórie sa pre rovinné rozhranie rovná ![]() . Ak je
. Ak je ![]() väčší v
porovnaní s polomerom krivosti rozhrania, bude
väčší v
porovnaní s polomerom krivosti rozhrania, bude ![]() . Nakoľko pri riešení difúznej rovnice môžeme
separovať premenné r a z,
. Nakoľko pri riešení difúznej rovnice môžeme
separovať premenné r a z, ![]() . Zasunutie riadiacej tyče do AZ nemá vplyv na
rozloženie hustoty toku neutrónov po výške AZ, t.j. na Z(z), potom sa axiálna
zložka úniku neutrónov rovná
. Zasunutie riadiacej tyče do AZ nemá vplyv na
rozloženie hustoty toku neutrónov po výške AZ, t.j. na Z(z), potom sa axiálna
zložka úniku neutrónov rovná 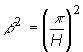 . Zasunutie tyče do zóny vyvolá však zmenu radiálnej
zložky funkcie rozloženia hustoty toku neutrónov
. Zasunutie tyče do zóny vyvolá však zmenu radiálnej
zložky funkcie rozloženia hustoty toku neutrónov ![]() . Obecné riešenie
. Obecné riešenie ![]() pre valcovú AZ má
tvar:
pre valcovú AZ má
tvar:
![]() (11.6)
(11.6)
Kde A a C sú
integračné konštanty a J0, Y0 sú Besselové funkcie
nultého rádu prvého a druhého druhu. Priebeh Besselových funkcií je na strane
90, obr.8.3.
Pre valcovú AZ
bez zasunutej riadiacej tyče z okrajovej podmienky na hranici AZ je
hustota toku neutrónov určená vzťahom:
![]() (11.7)
(11.7)
Integračnú
konštantu A určíme z výkonu reaktora. Po zasunutí riadiacej tyče
do AZ má rozloženie hustoty toku neutrónov tvar:
![]() (11.8)
(11.8)
Z okrajovej
podmienky na hranici AZ, kde sa ![]() , určíme pomer medzi integračnými konštantami A a
C. Teda ak r = R, potom pre
, určíme pomer medzi integračnými konštantami A a
C. Teda ak r = R, potom pre ![]() platí:
platí:
![]() (11.9)
(11.9)
Potom obecné
riešenie (11.8) má tvar :
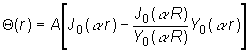 (11.10)
(11.10)
Hodnotu A
určíme z okamžitého výkonu v AZ. Pre veľký reaktor, kde R0
<< R, stačí malá zmena ![]() na to, aby sa AZ po
zasunutí riadiacej tyče stala kritickou.
na to, aby sa AZ po
zasunutí riadiacej tyče stala kritickou.
Nech ![]() je hodnota
je hodnota ![]() pre AZ s vysunutou
riadiacou tyčou. Parameter
pre AZ s vysunutou
riadiacou tyčou. Parameter ![]() - so zasunutou tyčou môžeme vyjadriť ako prírastok
nasledovne:
- so zasunutou tyčou môžeme vyjadriť ako prírastok
nasledovne:
![]() (11.11)
(11.11)
kde ![]() je malá hodnota.
je malá hodnota.
Besselové
funkcie vo vzťahu (11.10) potom môžeme zapísať v tvare:
![]() (11.12)
(11.12)
Pre kritický
reaktor bez regulačnej tyče je ![]() a
a ![]() . Hodnotu Besselové funkcie v argumente ktorej došlo
k malému nárastu, môžeme určiť ako prírastok hodnoty funkcie
nasledovne:
. Hodnotu Besselové funkcie v argumente ktorej došlo
k malému nárastu, môžeme určiť ako prírastok hodnoty funkcie
nasledovne:
![]() (11.13)
(11.13)
Pretože,
prírastok parametra ![]() je malé číslo,
hodnotu Besselovej funkcie druhého druhu, ktorá prechádza plochým maximom
(obr.8.3) platí:
je malé číslo,
hodnotu Besselovej funkcie druhého druhu, ktorá prechádza plochým maximom
(obr.8.3) platí:
![]() (11.14)
(11.14)
Pre malé
hodnoty r bude ![]() veľmi malé,
môžeme pre vyjadrenie Besselových funkcií používať asymptotické
vyjadrenie:
veľmi malé,
môžeme pre vyjadrenie Besselových funkcií používať asymptotické
vyjadrenie:
![]() (11.15)
(11.15)
![]() (11.16)
(11.16)
Ak dosadíme
vzťahy (11.15) a (11.16) do (11.10),
postupnými úpravami obdržíme:
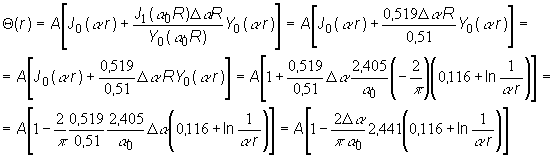
Prebytok multiplikačného koeficientu, ktorý je kompenzovaný riadiacou tyčou, je možné vyjadriť nasledovne:
![]() (11.17)
(11.17)
Kde k je
multiplikačný koeficient so zasunutou tyčou, a k0 s vysunutou tyčou. Pomocou kritickej
rovnice reaktora v jednoskupinovom priblížení môžeme pre AZ so zasunutou
tyčou zapísať:
![]() (11.18)
(11.18)
Pre AZ bez
tyče obdobne platí:
![]() (11.19)
(11.19)
Prírastok
hodnoty multiplikačného koeficienta sa potom bude rovnať:
![]() (11.20)
(11.20)
Z posledného
vzťahu vyjadríme podiel:
![]() (11.21)
(11.21)
Posledný
vzťah deľme hodnotou ![]() , potom obdržíme:
, potom obdržíme:
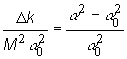 (11.22)
(11.22)
Vyjadrime
pravú stranu (11.22) pomocou prírastku parametra ![]() . Pre veľkosť rozmerov energetického reaktora je
prírastok parametra
. Pre veľkosť rozmerov energetického reaktora je
prírastok parametra ![]() malé číslo.
Parameter
malé číslo.
Parameter ![]() , pre AZ so zasunutou tyčou, je vyjadrený vzťahom
(11.11), druhá mocnina tohto parametra sa rovná:
, pre AZ so zasunutou tyčou, je vyjadrený vzťahom
(11.11), druhá mocnina tohto parametra sa rovná:
![]() (11.23)
(11.23)
Nakoľko
je hodnota prírastku parametra ![]() malé číslo, bude
jeho druhá mocnina veličinou ešte
podstatne menšou, takže ju vo vzťahu (11.23) môžeme zanedbať. Potom
platí:
malé číslo, bude
jeho druhá mocnina veličinou ešte
podstatne menšou, takže ju vo vzťahu (11.23) môžeme zanedbať. Potom
platí:
![]() (11.24)
(11.24)
Vzťah
(11.24) podelíme ![]() a obdržíme pravú
stranu (11.22), ktorú ďalej upravíme:
a obdržíme pravú
stranu (11.22), ktorú ďalej upravíme:
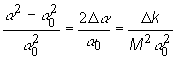 (11:25)
(11:25)
Vzťah
(11.25) dosadíme do výrazu pre radiálnu zložku hustoty toku neutrónov ![]() , vyjadrenú pomocou asymptotického tvaru Besselových funkcií,
potom obdržíme:
, vyjadrenú pomocou asymptotického tvaru Besselových funkcií,
potom obdržíme:
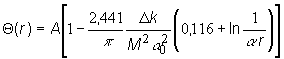 (11.26)
(11.26)
Na
extrapolovanom polomere absorpčnej tyče ![]() , sa hustota toku neutrónov rovná nule, preto po dosadení do
(11.26) platí:
, sa hustota toku neutrónov rovná nule, preto po dosadení do
(11.26) platí:
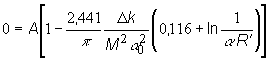 (11.27)
(11.27)
Za
predpokladu, že integračná konštanta A je rôzna od nuly, musí byť v
poslednom vzťahu rovný nule výraz v hranatej zátvorke, takže platí:
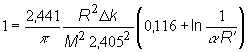 (11.28)
(11.28)
Zo vzťahu
(11.28) vyjadríme hľadanú hodnotu zmeny multiplikačného koeficienta ![]() vyvolanej zasunutím
centrálnej absorpčnej tyče do AZ:
vyvolanej zasunutím
centrálnej absorpčnej tyče do AZ:
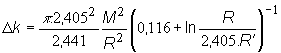 (11.29)
(11.29)
Po úprave
(11.29) pre prírastok multiplikačného koeficienta platí vzťah:
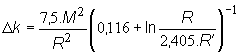 (11.30)
(11.30)
Efektívnosť
centrálnej regulačnej tyče je hodnota ![]() , o ktorú sa k0 zmení po zasunutí tyče do
centra AZ, je určená pomocou jednoskupinového priblíženia, má dva základné
nedostatky :
, o ktorú sa k0 zmení po zasunutí tyče do
centra AZ, je určená pomocou jednoskupinového priblíženia, má dva základné
nedostatky :
1) uvážením
len jednej skupiny neutrónov obdržíme väčšie pohltenie neutrónov v
absorpčnej tyči, čo dáva ![]() väčšie, ako je
skutočný prírastok multiplikačného koeficienta po zasunutí centrálnej
tyče do AZ;
väčšie, ako je
skutočný prírastok multiplikačného koeficienta po zasunutí centrálnej
tyče do AZ;
2) difúzna
rovnica nedáva presné riešenie v blízkom okolí poruchy, tj. kým r nie je väčšie ako (2 až 3) ![]() od miesta poruchy.
od miesta poruchy.
11.1.2
Efektívnosť regulačných tyčí
V jadrovom
reaktore sa nachádza niekoľko desiatok regulačných tyčí.
Konkrétne, v reaktore VVER-440 je umiestnených 37 regulačných kaziet.
Vzniká teda prirodzená požiadavka ocenenia efektívnosti regulačnej
tyče umiestnenej excentricky. Na ocenenie jej efektívnosti použijeme
závery teórie porúch. Efektívnosť
úplne zasunutej regulačnej tyče ![]() nachádzajúcej sa vo
vzdialenosti r, od osi symetrie homogénneho valcového reaktora, ,je závislá od
efektívnosti
nachádzajúcej sa vo
vzdialenosti r, od osi symetrie homogénneho valcového reaktora, ,je závislá od
efektívnosti ![]() tejto tyče
v strede AZ nasledovne:
tejto tyče
v strede AZ nasledovne:
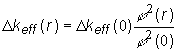 (11.31)
(11.31)
kde ![]() a
a ![]() sú hustoty toku
neutrónov na polomere r a v strede reaktora bez tyčí.
sú hustoty toku
neutrónov na polomere r a v strede reaktora bez tyčí.
V energetickom reaktore sú regulačné kazety rozmiestnené na rôznych koncentrických kružniciach o polomere r, potom ich celková efektívnosť je rovná sume:
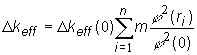 (11.32)
(11.32)
kde n je
počet skupín regulačných kaziet
m počet
kaziet v skupine
ri polomer, na ktorom sú rozmiestnené kazety i-tej skupiny
Pre homogénny
reaktor bez reflektora v tvare valca o polomere R, efektívnosť
systému regulačných kaziet môžeme určiť pomocou vzťahu:
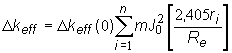 (11.33)
(11.33)
kde J0(r) je Besselová funkcia nultého rádu
Re extrapolovaný polomer reaktora Re=R+d;
ostatné symboly sú ako v (11.32)
Pre úplnosť je potrebné poznamenať, že celková účinnosť systému regulačných kaziet nemusí byť vždy rovná algebraickému súčtu efektívnosti jednotlivých kaziet. V závislosti od ich množstva, rozmiestnenia a postupnosti zasúvania môže byť celková efektívnosť systému regulácie väčšia alebo menšia ako súčet efektívností jednotlivých kaziet. Tento efekt sa nazýva interferenciou regulačných kaziet. Interferenciu kaziet je možné vysvetliť na základe už uvedeného nasledovne. Každá zasunutá regulačná tyč (kazeta) spôsobuje prerozdelenie hustoty toku neutrónov v reaktore. V blízkosti tyče sa hustota toku neutrónov znižuje a v miestach vzdialených od tyče, sa hustota toku neutrónov zväčšuje oproti stavu, keď v reaktore nebola zasunutá tyč. Preto efektívnosť tyče umiestnenej v blízkosti už zasunutej tyče bude menšia, v porovnaní s efektívnosťou tyče umiestnenej ďalej. Interferencia tyčí je vyjadrená koeficientom K, takže pre efektívnosť systému regulačných kaziet platí:
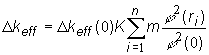 (11.34)
(11.34)
Regulačné
kazety , najmä šiesta skupina, obyčajne nie sú úplne zasunuté do AZ. Preto
je potrebné určiť efektívnosť regulačných kaziet
v závislosti od hĺbky ich zasunutia. Efektívnosť
čiastočne zasunutej regulačnej kazety môžeme určiť
pomocou už spomínanej teórie porúch
nasledovne:
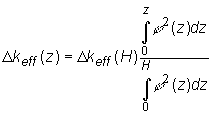 (11.35)
(11.35)
kde ![]() a
a ![]() sú
efektívnosti regulačných tyčí zasunutých do hĺbky z, respektívne
H
sú
efektívnosti regulačných tyčí zasunutých do hĺbky z, respektívne
H
![]() je rozloženie,
tyčou neovplyvnenej, hustoty toku neutrónov po výške reaktora
je rozloženie,
tyčou neovplyvnenej, hustoty toku neutrónov po výške reaktora
Rozloženie
hustoty toku neutrónov po výške reaktora je rovné:
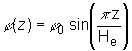 (11.36)
(11.36)
kde ![]() je hustota toku
neutrónov v počiatku súradnicového systému
je hustota toku
neutrónov v počiatku súradnicového systému
He je extrapolovaná výška reaktora He=H+2d
Ak do vzťahu(11.35) dosadíme výraz pre rozloženie hustoty toku neutrónov (11.36), urobíme integráciu a potrebné úpravy, obdržíme:
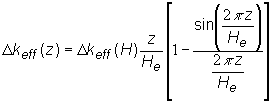 (11.37)
(11.37)
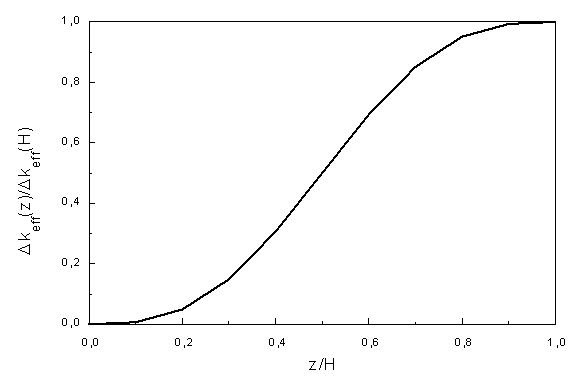
Efektívnosť
regulačnej tyče v závislosti od hĺbky zasunutia do AZ je na
obr.11.3.Táto závislosť sa nazýva integrálnou charakteristikou
regulačnej tyče.
Obr.11.3 Závislosť efektívnosti tyče od hĺbky
zasunutia do reaktora