12. Nestacionárny stav reaktora.

Doposiaľ sme všade uvažovali stacionárny stav reaktora, keď sa hustota neutrónov s časom nemenila. Teraz budeme skúmať stav reaktora, kedy sa hustota neutrónov s časom bude meniť. Táto zmena je následkom zmeny multiplikačného koeficientu, či už následkom vysunutia, respektíve zasunutia regulačnej (havarijnej ) tyče do AZ alebo vysunutím paliva a či oddialením reflektoru ako aj zmeny koncentrácie H3BO3 v chladive, či zmenou teploty štiepneho prostredia. Pre naše prvé úvahy budeme uvažovať, že v reaktore sú iba okamžité neutróny štiepenia. Doba života týchto, je daná dobou spomaľovania a dobou difúzie tepelných neutrónov. Pre tepelné reaktory je tdif >> tspomal. V závislosti od absorpčných vlastností AZ sa tdif = 10-5-10-3 sekundy.

12.1 Bodová kinetika na okamžitých neutrónoch

V ďalšom budeme predpokladať holý homogénny, tepelný reaktor a budeme riešiť diferenciálnu rovnicu v jednoskupinovom priblížení za predpokladu, že keff sa iba veľmi málo líši od jednotky. Vtedy pri riešení diferenciálnej rovnice môžeme zanedbať vyššie harmonické s dostatočnou presnosťou.

Zapíšeme si teraz difúznu rovnicu v nestacionárnom stave :

 

                                 (12.1)

kde zdroj neutrónov vyjadríme vzťahom: (12.2)

 

Do diferenciálnej rovnice (12.1) dosadíme vzťah (12.2) a delíme celú rovnicu hodnotou, čím obdržíme:

              (12.3)

Z predošlého vieme, že podiel  predstavuje kvadrát difúznej dĺžky L2 a podieľ  sa rovná strednej dobe difúzie tepelných neutrónov , ktorá vyjadruje strednú dobu života jedného pokolenia neutrónov v nekonečne veľkom prostredí a označujeme jú .Potom ma (12.3) tvar:

                 (12.4)

Riešme diferenciálnu rovnicu (12.4) separáciou premenných .

Na základe tohoto rovnicu upravíme na tvar :

                     (12.5)

Náš predpoklad je splnený, ľavá strana rovnice (12.5) závisí iba od polohy v reaktore r a pravá strana závisí len od času t, preto je separáciu možné uskutočniť. Ľavá aj pravá strana separovanej rovnice (12.5) je rovná konštante  – B2.

Ako sme predpokladali, zmena keff je malá. Rozloženie hustoty toku tepelných neutrónov  bezprostredne po zmene keff, ktorá platila pred zmenou, keď bol reaktor kritický, preto môžeme vyjadriť:

                                                (12.6)

Z posledného vzťahu vyjadríme podiel nazývaný tiež Laplacian:

                                                           (12.7)

Dosadíme (12.7) do rovnice (12.5) a po úprave obdržíme:

    (12.8)

Po úprave (12.8) platí:

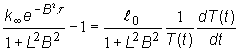           (12.9)

Prvý člen na ľavej strane tejto rovnice predstavuje keff a na pravej strane vyjadruje strednú dobu života jedného pokolenia neutrónov v prostredí konečných rozmerov , ďalej teda platí:

                                (12.10)

 

Teda v (12.9) označíme: 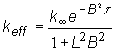, respektívne  

Zbytkový multiplikačný koeficient  vyjadrujúci odchýlku keff od kritického stavu označujeme:                                                                         (12.11)

Reaktivita sústavy je bezrozmerná veličina, udávajúca relatívnu zmenu keff do jednej tj. od kritického stavu.:

                                                  (12.12)

Čiže (12.10) môžeme zapísať v tvare:

                                           (12.13)

Po úprave platí:

                                                (12.14)

Riešením diferenciálnej rovnice (12.14) obdržíme funkciu časovej zmeny hustoty toku neutrónov v každom bode aktívnej zóny reaktora v tvare:

                                                 (12.15)

Riešenie rovnice (12.4), vyjadrujúce zmenu hustoty toku neutrónov v reaktore bez uváženia oneskorených neutrónov, obdržíme ak rovnicu (12.15) vynásobíme priestorovou zložkou funkcie hustoty toku neutrónov R(r):

                                                   (12.16)

V čase t = 0, keď došlo k zmene keff , bola hustota toku neutrónov rovná . Označíme hodnotu hustoty toku neutrónov na počiatku zmeny ako , potom platí:

                                                        (12.17)

Perióda reaktora vyjadruje strmosť exponenciálnej zmeny hustoty toku neutrónov, ale aj výkonu v aktívnej zóne, v závislosti od času. Podľa definície ,je perióda reaktora doba, za ktorú výkon, respektívne hustota toku neutrónov, vzrastie e-krát. Teda, ak sa t=T, bude platiť:

                                                               (12.18)

Zo vzťahu (12.17) pre periódu reaktora vyplýva:

                                                                                  (12.19)

V reaktorovej technike sa okrem periódy používa aj pojem doba zdvojeniaT2 .Dobou zdvojenia rozumieme časový úsek, za ktorý sa výkon alebo hustota toku neutrónov v reaktore zvýši dvojnásobne. Podobne môžeme z rovnice (12.17) pre t=T2 vyjadriť pomer:

                                                             (12.20)

Doba zdvojenia sa potom rovná:

, alebo     , či        (12.21)

Z uvedeného vyplýva, čím je  menšie, bude perióda reaktora kratšia a čím je  väčšie, tým je T menšia.

Uvažujme nestacionárny stav reaktora charakterizovaný zbytkovým multiplikačným koeficientom  a strednou dobou života jedného pokolenia neutrónov

 = 0,001 s, potom je perióda reaktora rovná .

To znamená, že v takejto sústave za 0,1 sekundy výkon vzrastie e-krát a za 1 sekundu hustota toku tepelných neutrónov vzrastie e10-krát čo je 2.104 násobok pôvodnej hodnoty.výkonu.

12.2 Difúzna rovnica s oneskorenými neutrónmi.

Z predchádzajúcich úvah vieme, že v prípade existencie len okamžitých neutrónov je perióda reaktora veľmi malá, to znamená, že časová zmena hustoty neutrónového toku je veľmi prudká. Riadiť takú sústavu by nebolo možné. Našťastie okrem okamžitých neutrónov vznikajú pri štiepení ťažkých jadier aj oneskorené neutróny. Ako už bolo uvedené, podiel týchto neutrónov, pri štiepení , je  z celkového počtu vznikajúcich neutrónov. Bolo pozorované šesť skupín týchto neutrónov a každá skupina je charakterizovaná - relatívnym množstvom oneskorených neutrónov i-tej skupiny a ti - strednou dobou života predchodcov materských jadier oneskorených neutrónov i-tej skupiny. Platí 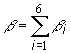. Doba života predchodcu materského jadra oneskorených neutrónov aj tej najkratšie žijúcej skupiny je podstatne väčšia ako doba života okamžitých neutrónov (uvažujeme len dobu difúzie).

Priemerná doba oneskorenia pre oneskorené neutróny i-tej skupiny je daná súčinom .Celkovú priemernú dobu oneskorenia určíme ako súčet  všetkých skupín oneskorených neutrónov, teda je rovná .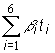

Ak uvažujeme ako dobu života jedného pokolenia dobu difúzie, potom celková stredná doba života neutrónov, okamžitých a oneskorených, sa rovná súčtu:

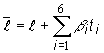                                                                    (12.22)

kde      je priemerná doba života okamžitých tepelných neutrónov,

sumárna doba oneskorenia je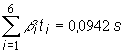 čo je zhruba 0,1 sek.

Pretože, doba života okamžitých neutrónov v relatívne slabo absorbujúcom prostredí má hodnotu  = 10-3 s, môžeme ju zanedbať v porovnaní s 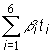, ktorú budeme považovať za strednú dobu života jedného pokolenia neutrónov. Určime teraz hodnotu periódy prechodového procesu pre podobný prípad vnosu kladnej hodnoty zbytkového multiplikačného koeficienta ako v predchádzajúcom prípade.

Nech ; stredná doba života neutrónov ; potom perióda reaktora bude . Takúto sústavu je možné riadiť veľmi dobre.

Napíšeme teraz diferenciálnu rovnicu difúzie v nestacionárnom stave:

                                             (12.23)

V predchádzajúcich úvahách sme počítali iba s okamžitými neutrónmi, vtedy zdroj neutrónov mal tvar . Teraz je potrebné nájsť nové vyjadrenie pre zdroj neutrónov, ktorý uvažuje aj s oneskorenými neutrónmi. Zdroj neutrónov je v reálnych podmienkach rovný súčtu okamžitých a oneskorených neutrónov:

                                                                                 (12.24)

V reaktore vzniká -tý diel okamžitých neutrónov a -tý diel oneskorených neutrónov. Preto výraz pre zdroj okamžitých neutrónov bude mať tvar:

                                                            (12.25)

Zostáva nám určiť zdroj oneskorených neutrónov. Rýchlosť vzniku neutrónov, ako okamžitých, tak aj oneskorených, je určená množstvom absorbovaných neutrónov v 1 cm3 za 1 sekundu, ktorá je rovná súčinu , alebo rýchlosťou vzniku rýchlych neutrónov. Rýchlosť vzniku predchodcov oneskorených neutrónov i-tej skupiny, je rovná súčinu  Označme koncentráciu predchodcov i-tej skupiny oneskorených neutrónov ako Ci(r,t), potom rýchlosť rozpadu predchodcov i-tej skupiny je rovná súčinu rozpadovej konštanty a koncentrácie predchodcov i-tej skupiny, tj. . Rýchlosť zmeny koncentrácie predchodcov materských jadier i-tej skupiny oneskorených neutrónov je vyjadrená ako rozdiel rýchlostí ich vzniku a zániku v jednotke objemu, tj. môžeme napísať nasledovnú diferenciálnu rovnicu:

                                       (12.26)

Je potrebné si uvedomiť, že koncentráciu predchodcov materských jadier oneskorených neutrónov všetkých šiestich skupín je potrebné určiť riešením sústavy šiestich diferenciálnych rovníc, formálne zhodných s (12.26). Rýchlosť rozpadu predchodcov materských jadier i-tej skupiny oneskorených neutrónov je rovná rýchlosti vzniku oneskorených neutrónov i-tej skupiny (okamžite po rozpade predchodcu, sú emitované oneskorené neutróny). Čiže rýchlosť vzniku oneskorených neutrónov je sumárne rovná 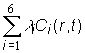. Ak vynásobíme tento člen pravdepodobnosťou neuniknutia oneskorených neutrónov zo štiepneho prostredia v procese spomaľovania  a pravdepodobnosťou úniku rezonančnému zachyteniu, obdržíme vyjadrenie pre zdroj oneskorených neutrónov:

                                                                      (12.27)

Pre jednoduchosť predpokladajme, že spektrum oneskorených neutrónov je rovnaké ako spektrum okamžitých neutrónov tj. . Hoci v skutočnosti je  menší ako , nakoľko kinetická energia oneskorených neutrónov je rovná 0,5 MeV, kým u okamžitých neutrónov sa rovná 2 MeV. Takýmto spôsobom sme zväčšili únik oneskorených neutrónov voči skutočnosti, čo by nám výrazne ovplyvnilo podiel oneskorených neutrónov v štiepnom prostredí. Zvýšený únik oneskorených neutrónov vykompenzujeme úmerným zvýšením podielu vznikajúcich oneskorených neutrónov. Zvýšený podiel oneskorených neutrónov nazývame efektívnym podielom oneskorených neutrónov . Hodnotu efektívneho podielu oneskorených neutrónov určíme pomocou vzťahu:

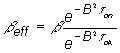                                                                            (12.28)

Veľkosť podielu pravdepodobností neuniknutia oneskorených a okamžitých neutrónov pri spomaľovaní, závisí od veľkosti reaktora. Pre energetické reaktory, charakterizované malým geometrickým parametrom B2, má tento pomer hodnotu 1,1 až 1,15 a pri experimentálnych reaktoroch sa tento pomer rovná 1,2 až 1,25. Z uvedeného vyplýva, že podiel oneskorených neutrónov je potrebné, v závislosti do veľkosti reaktora, zvýšiť o 10% až 25%. Preto v ďalšom bude vystupovať už iba efektívny podiel oneskorených neutrónov, a to aj pre jednotlivé skupiny oneskorených neutrónov. S konečnou platnosťou môžeme člen vyjadrujúci zdroj neutrónov zapísať v tvare:

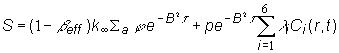                                 (12.29)

Teda diferenciálna rovnica popisujúca bilanciu neutrónov v nestacionárnom stave má tvar:

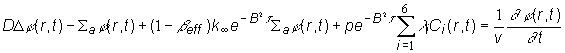(12.30

Rovnicu (12.30) podelíme makroskopickým účinným prierezom absorpcie  a úpravou obdržíme:

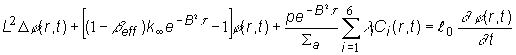            (12.31)

Diferenciálnu rovnicu (12.31) budeme riešiť separáciou premenných, tj. platí:

                                                                            (12.32)

                                                                        (12.33)

Vzťahy (12.32) a (12.33) dosadíme do rovnice (12.31), po úprave obdržíme diferenciálnu rovnicu v tvare:

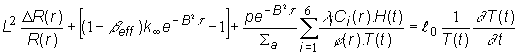           (12.34)

Premenné môžeme separovať, lebo  nezávisí od r, pretože koncentrácia predchodcov materských jadier oneskorených neutrónov je vždy proporciálna hustote toku tepelných neutrónov, tj. . Predpokladajme, že v čase t = 0 nastala náhla (skoková) zmena multiplikačného koeficienta k o malú hodnotu. Ak od tejto zmeny uplynie krátky čas, potom rozloženie hustoty toku tepelných neutrónov bude podobné jeho rozloženiu pred zmenou multiplikačného koeficienta. Z matematiky je známe, že dva podobné priebehy funkcií sú popísané rovnakými diferenciálnymi rovnicami. Preto na počiatku prechodového deja platí rovnaká diferenciálna rovnica, popisujúca priestorové rozloženie hustoty toku tepelných neutrónov, ako v stacionárnom stave, ktorý predchádzal zmenu k, tj. platí:

                                                                        (12.35)

Ak poslednú rovnicu vynásobíme časovou zložkou hustoty toku neutrónov T(t), obdržíme vyjadrenie diferenciálnej rovnice (12.23) v stacionárnom tvare:

                                                                    (12.36)

Z rovnice (12.36) vyjadríme Laplacián:

                                                                                 (12.37)

Rovnice (12.26) a (12.34) po separácii premenných a dosadení Laplaciánu z (12.37), sú lineárnymi diferenciálnymi rovnicami prvého rádu, môžeme teda ich riešenie navrhnúť v tvare :

                                                                                 (12.38)

Kde    

                                                                             (12.39)

Kde    

Rovnica (12.26), vyjadrujúca rýchlosť zmeny koncentrácie predchodcov i-tej skupiny oneskorených neutrónov ma tvar:

                                               (12.40)

Navrhnutý tvar riešenia sústavy lineárnych diferenciálnych rovníc, vyjadrený vzťahom (12.38) a (12.39), dosadíme do poslednej rovnice:

                                   (12.41)

Vzťah pre Cio vyjadríme z (12.41) úpravou nasledovne:

                                                                      (12.42)

Rovnicu (12.34) po separácii premenných zapíšeme v tvare:

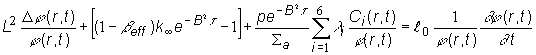(12.43)

Prvý sčítanec na ľavej strane (12.43) je Laplacián (12.31) rovný konštantnej hodnote –B2, jeho dosadením a úpravou obdržíme:

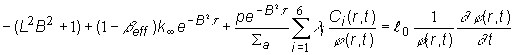(12.44)

Navrhnutý tvaru riešenia lineárnych diferenciálnych rovníc (12.38) a (12.39) dosadíme aj do poslednej rovnice:

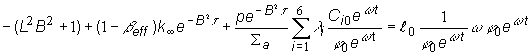(12.45)

Úpravou a dosadením vzťahu (12.42) obdržíme:

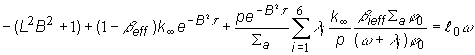           (12.46)

Ďalej upravíme (12.46):

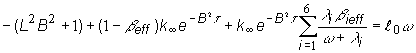  (12.47)

Rovnicu (12.47) vynásobíme pravdepodobnosťou neuniknutia neutrónov zo štiepneho prostredia v procese difúzie , a obdržíme:

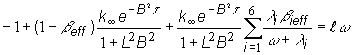      (12.48)

kde              je stredná doba života okamžitých neutrónov v štiepnom prostredí konečných rozmerov, podobne ako v predošlej kapitole;

Vzťah (12.48) ďalej upravíme, s využitím výrazu pre efektívny multiplikačný súčiniteľ keff, platí:

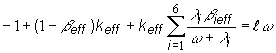                         (12.49)

Postupnými úpravami (12.49) obdržíme výraz pre zbytkový multiplikačný koeficient, nasledovne platí:

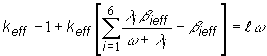                           (12.50)

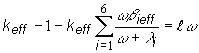                                            (12.51)

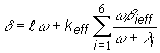                                                      (12.52)

Reaktivita sústavy je definovaná vzťahom:

                                                                         (12.53)

Použijeme definičný vzťah pre reaktivitu, takto úpravou (12.52) obdržíme charakteristickú rovnicu:

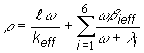                                                                   (12.54)

Posledný vzťah upravíme tak, že keff vyjadríme z definície reaktivity a dosadíme:

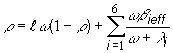                                                               (12.55)

Charakteristická rovnica bude mať po úprave nasledovný tvar:

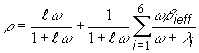                                                        (12.56)


Obdržali sme charakteristickú rovnicu, ktorá udáva závislosť parametra  na jadrových vlastnostiach materiálov aktívnej zóny. Uvedená rovnica je algebraickou rovnicou (6+1)-ho stupňa vzhľadom na . Pre danú hodnotu reaktivity existuje (6+1) hodnôt parametra . Obecný charakter riešenia rovnice (12.56) je možné najlepšie objasniť pomocou grafického znázornenia závislosti funkcie reaktivity od parametra .

 


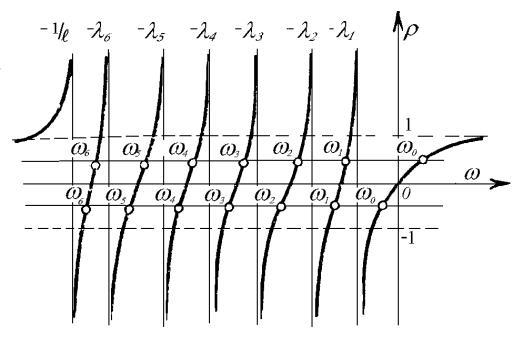
Obr.12.1 Závislosť reaktivity od časovej konštanty

Z obr.12.1 je zrejmé, že vnesením kladnej reaktivity do štiepnej sústavy > 0 má charakteristická rovnica sedem koreňov, z ktorých  je kladný, ostatné  až  sú záporné korene a sú približne rovné hodnotám . Ak do systému vnesieme zápornú reaktivitu r < 0, budú všetky korene charakteristickej rovnice záporné, t.j. aj w0<0. Riešením sústavy diferenciálnych rovníc (12.26) a (12.30) obdržíme časovú závislosť hustoty toku neutrónov v ľubovoľnom bode reaktora ako súčet siedmich exponenciálnych funkcií:

                (12.57)

Integračné konštanty A0, A1,.........., A6 určíme pomocou okrajových podmienok. Ďalej rozoberieme prípad kladnej vnesenej reaktivity. Vzhľadom na to, že všetky sčítance  okrem prvého na pravej strane rovnice (12.57) obsahujú exponenty so záporným znamienkom, je zrejmé, že hodnota týchto sčítancov s rastúcim časom postupne klesá až po uplynutí doby rádu , budú tieto sčítance rovné nule. V čase  a väčšom, bude časová zmena hustoty toku neutrónov v každom mieste reaktora rovná:

                                                                               (12.58)

Integračnú konštantu A0 určíme z počiatočnej podmienky nasledovne:

ak        bude sa hustota toku neutrónov rovnať .

Pre časovú zmenu hustoty toku neutrónov v čase  a väčšom potom platí:

                                                                               (12.59)

Časová konštanta  má rozmer obrátenej hodnoty času, preto jej obrátenú hodnotu nazývame ustálenou periódou reaktora:

                                                                                            (12.60)

Časová závislosť hustoty toku neutrónov, vyjadrená pomocou ustálenej periódy reaktora, bude mať tvar:

                                                                                 (12.61)

Podobne ako ustálenú periódu reaktora môžeme pomocou časových konštánt  až  vyjadriť prechodové periódy reaktora:

                                                             (12.62

Prechodové periódy majú vždy zápornú hodnotu, preto ich nemôžeme považovať za periódy reaktora v tom zmysle ako ustálenú periódu reaktora T.


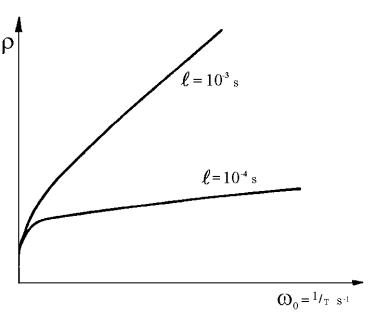
Závislosť časovej konštanty w0 od kladnej hodnoty reaktivity je podľa vzťahu (12.56) znázornená graficky na obr.12.2 za predpokladu, že stredná doba života okamžitých neutrónov  postupne nadobúda hodnoty 10-3 a 10-4 s. Hodnoty podielu oneskorených neutrónov bi a rozpadových konštánt predchodcov materských jadier oneskorených neutrónov li sú pre štiepny izotop 235U.

Obr.12.2 Závislosť reaktivity od recipročnej hodnoty ustálenej periódy reaktora

Z obr.12.2 je zrejme, že pri vnesení malej kladnej reaktivity r»0,005, krivky takmer splývajú. To znamená, pri malej reaktivite ustálená perióda reaktora nezávisí od strednej doby života okamžitých neutrónov . Pri väčšej kladnej reaktivite hodnota časovej konštanty w0 rastie (ustálená perióda reaktora T sa zmenšuje) so zmenšovaním strednej doby života okamžitých neutrónov.

Ak do reaktora vnesieme zápornú reaktivitu, budú mať všetky korene charakteristickej rovnice (12.56) zápornú hodnotu. Závislosť hustoty toku neutrónov od času bude ako v predošlom vyjadrená vzťahom (12.57). Všetky sčítance budú mať v exponente zápornú hodnotu, tj. všetky sa s rastúcim časom budú zmenšovať, až hustota toku neutrónov nadobudne nulovú hodnotu. Ustálená časť poklesu hustoty toku neutrónov bude určovaná prvým sčítancom, ako pri kladnej reaktivite v sústave, ktorý má v exponente najmenšiu hodnotu. Aj v tomto prípade hovoríme o ustálenej perióde, lebo charakterizuje ustálenú časť prechodového procesu v reaktore. Pri pozornom štúdiu charakteristickej rovnice zistíme, že vnesením rovnakej reaktivity, čo do absolútnej hodnoty, obdržíme dve rôzne veľkosti časovej konštanty w0. Pri vnesení kladnej reaktivity bude  väčšie, čo do absolútnej hodnoty, ako pri vnesení rovnako veľkej zápornej reaktivity. Teda rozdielna bude strmosť nárastu a poklesu hustoty toku neutrónov. Dané konštatovanie je zrejmé z obr.12.1 v prípade vnesenia reaktivity r=±1, v prípade kladnej hodnoty reaktivity sa koreň charakteristickej rovnice w0  blíži do nekonečna, kým pri zápornej reaktivite sa w0  ® -l1.Rozpadová konštanta najdlhšie žijúcej skupiny oneskorených neutrónov l1 určuje strmosť poklesu hustoty toku neutrónov pri odstavení reaktora vnesením veľkej zápornej reaktivity. Keďže  táto skupina oneskorených neutrónov má strednú dobu oneskorenia rovnú » 56 s, bude aj perióda  poklesu hustoty toku neutrónov rovná 56 s. Z uvedeného vyplýva, že strmosť poklesu hustoty toku neutrónov je menšia ako strmosť nárastu hustoty toku neutrónov pri vnesení rovnakej reaktivity čo do veľkosti, ale opačného znamienka. Tieto skutočnosti musíme brať do úvahy pri prevádzke jadrového reaktora. V ďalšom postupne rozoberieme fyzikálny význam najdôležitejších, vyššie odvodených vzťahov.

12.3 Vzorec „ prevrátenej hodiny “

Charakteristickej rovnici (12.54) vyhovujú všetky korene w0 až w6 . Pri zmene výkonu je určujúcim prvý sčítanec vzťahu (12.57), preto budeme hľadať súvis medzi hodnotou vnesenej reaktivity a ustálenou periódou reaktora. Dosaďme teda najmenší, čo do absolútnej hodnoty, koreň w0 do (12.54):

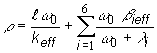                                                                              (12.63)

Do vzťahu (12.63) dosadíme namiesto w0 z (12.60) ustálenú periódu reaktora , potom platí:

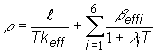                                                                   (12.64)

Výraz (12.64) vyjadruje súvis medzi reaktivitou a ustálenou periódou reaktora, často sa nazýva vzorcom prevrátenej hodiny. Podľa veľkosti ustálenej periódy reaktora môžeme usudzovať o veľkosti reaktivity, ktorá prechodový proces v reaktore vyvolala. Jedna z metód na určovanie veľkosti reaktivity je metóda merania ustálenej periódy reaktora ,ktorá sa opiera o uvedený vzťah. Hovoríme, že sústava má reaktivitu prevrátenej hodiny , ak ustálená perióda reaktora je rovná 1 hodine. Do (12.64) v tomto prípade dosadíme T=3600 s, nakoľko rozpadové konštanty  sú uvedené v s-1, potom obdržíme:

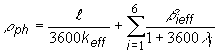                                                   (12.65)

Vzťah pre výpočet reaktivity v prevrátených hodinách r* dostaneme, ak výraz (12.64) podelíme (12.65):

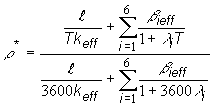                                                     (12.66)

Potom ľubovoľnú reaktivitu môžeme určiť ako súčin  t.j. . V ďalšom sa budeme zapodievať dvoma medznými prípadmi, pre ktoré je možné odvodiť jednoduchý výraz pre ustálenú periódu reaktora, ktorá vznikne po zániku prechodových členov.

12.4 Malá reaktivita

Rozoberieme prípad, keď zbytkový multiplikačný koeficient  a reaktivita  majú malé. kladné hodnoty. Zaujíma nás, aká bude hodnota ustálenej periódy reaktora, a ktoré z neutrónov na ňu budú dominantne vplývať. Z obr.12.1 je zrejmé, že pri malej vnesenej reaktivite  bude malý aj kladný koreň charakteristickej rovnice . Charakteristická rovnica s dosadeným koreňom  má tvar (12.63):

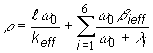
Keďže  je malé v porovnaní s ľubovolným , zanedbáme ho v menovateli výrazu . Potom pre ustálenú periódu platí :

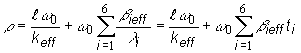                               (12.67)

kde     ti          je stredná doba života predchodcov materských jadier i-te skupiny oneskorených neutrónov;

                     je stredná doba života okamžitých neutrónov;

Do posledného vzťahu dosadíme namiesto , takže platí:

                                                                 (12.68)

Zo vzťahu (12.68) vyjadríme ustálenú periódu reaktora:

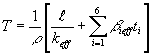                                                                    (12.69)

Ak uvažujeme len dobu difúzie tepelných neutrónov, potom sa táto nachádza v medziach od10-3 až do 10-5 s. Pretože vnesená reaktivita  je malá, bude sa keff len veľmi málo líšiť od jednej. Výraz  nadobudne takto svoju maximálnu hodnotu rovnú 10-3 s. Vieme, že suma 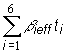 znamená celkovú priemernú dobu oneskorenia neutrónov a tá má pre  hodnotu rovnú 0,0942 s. Preto vo výraze (12.69) zanedbáme prvý člen v hranatých zátvorkách a obdržíme vzťah pre ustálenú periódu reaktora:

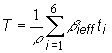                                                                              (12.70)

Pri našich úvahách sme predpokladali, že kladný koreň charakteristickej rovnice  je podstatne menší ako rozpadová konštanta predchodcov materských jadier  ktorejkoľvek skupiny oneskorených neutrónov.. Preto ustálená perióda reaktora  musí byť väčšia ako stredná doba života predchodcov materských jadier ktorejkoľvek skupiny oneskorených neutrónov. Maximálna hodnota ti je rovná až 56,6 s, preto ustálená perióda reaktora T je väčšia i od tejto hodnoty. Pre určitú malú hodnotu reaktivity a daný palivový materiál je perióda ľubovoľného tepelného reaktora stála a nezávisí od doby života okamžitých neutrónov.

12.5 Veľká reaktivita

Teraz uvážime druhý krajný prípad, keď reaktivita sústavy bude veľmi veľká, potom vo vzťahu (12.63) bude každé  menšie ako , viď obr.12.1. Nakoľko v tomto prípade platí, že <<, potom môžeme v menovateli vzťahu (12.63)  zanedbať. Potom pre reaktivitu vyjadrenú uvedeným vzťahom platí:

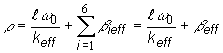                                                              (12.71)

Dosadíme teraz namiesto  z výrazu (12.60) periódu reaktora, potom pre veľkú vnesenú reaktivitu platí:

                                                                                         (12.72)

Z (12.72) vyjadríme ustálenú periódu reaktora:

                                                                                       (12.73)

Výraz (12.73) má význam, len ak je hodnota vnesenej reaktivity väčšia ako efektívny podiel oneskorených neutrónov tj. > a > 0. Ak je vnesená reaktivita väčšia ako , potom môžeme podiel oneskorených neutrónov zanedbať. Za týchto podmienok pre ustálenú periódu reaktora platí vzťah:

                                                                                                   (12.74)

To znamená, že ustálená perióda reaktora je pri vnose veľkej kladnej reaktivity do reaktora určovaná dobou života okamžitých neutrónov. Z hľadiska regulácie reaktora je toto stav, keď reaktor už nie je možné kontrolovať. Stavu, keď ustálená perióda reaktora je určovaná iba okamžitými neutrónmi, sa v prevádzke reaktora nesmieme ani len priblížiť.

Stavu reaktora, keď ustálená perióda práve prestane závisieť od doby oneskorenia , hovoríme kritičnosť na okamžitých neutrónoch. Vtedy je vnesená reaktivita rovná efektívnemu podielu oneskorených neutrónov, tj.. Hodnota efektívneho podielu oneskorených neutrónov  pre energetické reaktory s palivom obohateným na 4% izotopom  je » 0,007. Reaktivita rovná práve efektívnemu podielu oneskorených neutrónov sa označuje ako jednotka reaktivity jeden dolár.


 


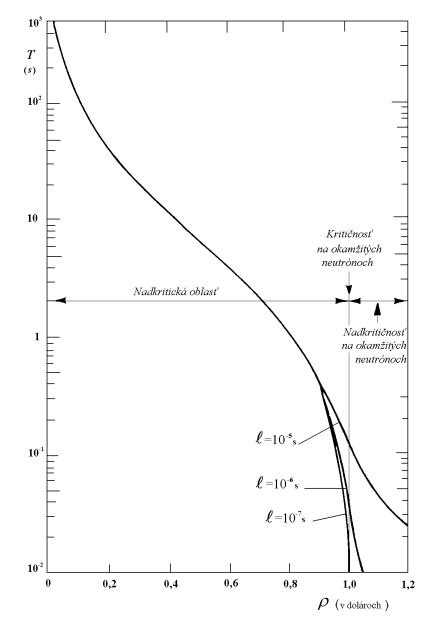
Obr.12.3 Závislosť ustálenej periódy reaktora od reaktivity.

V reaktorovej technike sa jednotka reaktivity dolár často používa najmä pri meraní reaktivity metódou pádu tyče (Rod Drop), či meraní pomocou reaktimera a pod. Ľubovoľnú reaktivitu môžeme vyjadriť v dolároch ako podiel reaktivity v absolútnej hodnote k efektívnemu podielu oneskorených neutrónov, tj. platí:

r($) =                                                                                      (12.75)

Absolútnu hodnotu reaktivity dostaneme, ak reaktivitu v dolároch vynásobme efektívnym podielom oneskorených neutrónov:

r=r($).beff                                                                                        (12.76)

Z definície  vyplýva, že pre kritičnosť na okamžitých neutrónoch je potrebné, aby sa reaktivita rovnala efektívnemu podielu oneskorených neutrónov, tj. . Ak je keff menšie ako , potom je perióda reaktora ovplyvnená oneskorenými neutrónmi, ale čím sa viac blíži k tejto hodnote, tým menej vplývajú oneskorené neutróny na ustálenú periódu prechodového procesu.

Na obr.12.3 je znázornená závislosť ustálenej periódy reaktora od reaktivity pre rôzne doby života okamžitých neutrónov: 1 - =10-5s; 2 - =10-6s; 3 - =10-7s. Z obrázku je zrejmé, že do hodnoty reaktivity vnesenej do reaktora rovnej približne r=0,9 $, ustálená perióda reaktora nezávisí  od doby života okamžitých neutrónov, je teda určovaná iba dobou života oneskorených neutrónov. Na obrázku je vyznačená oblasť nadkritičnosti reaktora na okamžitých neutrónoch ako aj stav keď sa reaktor stane kritický na okamžitých neutrónoch. Ako už bolo uvedené, takýto stav reaktora je v prevádzke neprípustný.

 

12.6 Kinetické rovnice reaktora

Štúdium prechodových procesov v jadrových reaktoroch vo väčšine prípadov používa jednoskupinovú difúznu teóriu. Priestorové rozloženie hustoty toku neutrónov budeme považovať za nemenné. V prípade porušenia kritického stavu bude nastávať zmena hustoty toku neutrónov v každom bode priestoru AZ rovnako. Budeme používať tzv. bodový model kinetiky, umožňujúci popísať časový priebeh hustoty toku neutrónov v reaktore pomocou sústavy lineárnych diferenciálnych rovníc prvého rádu.

12.6.1                  Rovnice kinetiky bez uváženia oneskorených neutrónov

 

Predpokladajme, že pri štiepení vznikajú iba okamžité neutróny. Časový priebeh hustoty toku neutrónov je určený riešením diferenciálnej rovnice pre jednu skupinu neutrónov – tepelnú skupinu neutrónov.

                                                                 (12.77)

Rovnicu (1) riešime metódou separácie premenných

                                                                                           (12.78)

Po dosadení (2) do (1) obdržíme

                                                       (12.79)

Vydelíme (12.79) súčinom  a obdržíme

                                                                      (12.80)

Ďalej rovnicu (12.80) upravíme na tvar

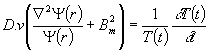                                                                    (12.81)

Ľavá aj pravá strana rovnice (12.81) sa rovná rovnakej konštante, ktorú si označíme . Kladná hodnota  by nás priviedla k riešeniu, ktoré je v rozpore so skutočným priebehom hustoty toku neutrónov.

Takto máme namiesto parciálnej diferenciálnej rovnice premenných r a t, dve diferenciálne rovnice

                                                                                             (12.82)

a

                                                                     (12.83)

Priestorová zložka hustoty toku neutrónov predstavuje vlastné funkcie riešenia vlnovej rovnice

                                                                                 (12.84)

kde  sú vlastné čísla. Napríklad v reaktore tvaru nekonečnej dosky o hrúbke H sú vlastné funkcie rovníc

                                                                                             (12.85)

a vlastné čísla tvoria postupnosť

                                                                                (12.86)

Porovnaním rovníc (12.83) a (12.84) je zrejmé, že každému vlastnému číslu  odpovedá parameter , t.j.

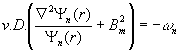                                                                           (12.87)

V rovnici (12.87) je podiel  na základe (12.84) rovný , teda

                                                                                        (12.88)

Potom riešenie nestacionárnej difúznej rovnice (12.77) v jednoskupinovom priblížení môžeme zapísať v nasledovnom tvare

                                                                             (12.89)

Nakoľko vlastné čísla obecne spĺňajú nerovnosť

 platí aj

Z uvedeného vyplýva, že vplyv vyšších zložiek po krátkom čase zanikne a časový priebeh hustoty neutrónového toku je určovaný v prevažnej miere prvým členom súčtu (13). Vhodným predpokladom pre vyjadrenie priestorového rozloženia je

                                                                                       (12.90)

Podľa tohto predpokladu sa priestorové rozloženie hustoty toku neutrónov v priebehu prechodového procesu nemení a je určené vlastnou funkciou , odpovedajúcou priestorovému rozloženiu v kritickom stave.

Po dosadení (12.90) do (12.77) obdržíme

                                                                                             (12.91)

Nakoľko  a  je

                                                               (12.92)

Ďalej upravíme vzťah (12.92) nasledovne

                                             (12.93)

Nakoľko  bude mať (12.93) nasledovný tvar

                                              (12.94)

kde  - predstavuje dobu života okamžitých neutrónov v nekonečnej sústave. Zo vzťahu (12.94) na pravej strane vyjmeme pred zátvorku člen  a obdržíme

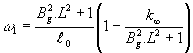                                                                        (12.95)

Stredná doba života jedného pokolenia okamžitých neutrónov v sústave konečných rozmerov sa rovná

Takto vzťah (12.95) nadobudne tvar

                                                                             (12.96)

Rovnica kinetiky bez vplyvu oneskorených neutrónov má potom tvar

                                                                                        (12.97)

Hustota neutrónov n(t) môže byť normovaná ľubovolne. Nakoľko hustota neutrónov je úmerná hustote výkonu Q(t) podľa vzťahu

                                                                                    (12.98)

kde Ef – energia uvolnená pri štiepení jedného jadra

  - makroskopický účinný prierez štiepenia

 v – rýchlosť neutrónov

môžeme rovnicu (12.97) zapísať v tvare

                                                                                      (12.99)

Ak výkonová hustota a podobne aj výkon celej AZ je v čase t = 0 rovný Q0, potom časový priebeh výkonu je určovaný rovnicou

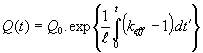                                                                     (12.100)

Ak sa v čase t = 0 zmení keff na konštantnú hodnotu rôznu od jednej, bude mať (12.100) tvar

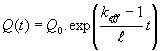                                                                                (12.101)

 

12.6.1.1Perióda reaktora

 

            Doba za ktorú sa zvýši hustota neutrónov, hustota toku neutrónov, výkonová hustota v danom mieste, alebo výkon reaktora e-krát sa nazýva periódou reaktora. Ak predpokladáme, že pri štiepení vznikajú iba okamžité neutróny, je časový priebeh výkonu určovaný rovnicou (12.101). Pri skokovej zmene reaktivity je perióda reaktora T rovná

                                                                                                     (12.102)

V tlakovodnom reaktore je stredná doba života okamžitých neutrónov rovná rádovo 10-4 s. V prípade, že sa efektívny multiplikačný koeficient skokom zvýši z 1 o 0,1% t.j. na keff = 1,001, bude podľa (12.102) perióda reaktora rovná 0,1 s. To znamená, že výkon reaktora sa za každú desatinu sekundy zvýši e-krát. Za jednu sekundu takto výkon narastie . Z uvedeného vyplýva, že pri takýchto prudkých zmenách výkonu je riadenie reaktora veľmi obtiažne až nemožné.

Priebeh prechodového procesu našťastie významne ovplyvňujú oneskorené neutróny. Aj keď je ich podiel pri štiepení pomerne malý, podstatne predlžujú strednú dobu života jednej generácie neutrónov v reaktore, nakoľko sa objavujú v štiepnej sústave s určitým oneskorením rovným strednej dobe života materských jadier . Ak zanedbáme dobu spomaľovania, môžeme vyjadriť strednú dobu života jednej generácie ako súčet

                                                                                       (12.103)

Suma  určuje strednú dobu oneskorenia všetkých skupín oneskorených neutrónov a pre štiepny systém s 5U je rovná 0,0942 s. Stredná doba oneskorenia  je zhruba o tri rády väčšia ako stredná doba života okamžitých neutrónov. V takomto prípade sa rovnakým spôsobom predĺži aj perióda reaktora z 0,1 s na T» 100 s. Sústava s periódou » 100 s je vhodná na riadenie štiepneho procesu.

Blahodárny vplyv  oneskorených neutrónov na prechodový proces sa prejavuje len pri malých zmenách reaktivity, keď štiepenie vyvolané oneskorenými neutrónmi predstavuje príspevok, bez ktorého nemôže byť dosiahnutá vyvážená bilancia neutrónov (kritický stav). Ak je vnesená reaktivita  je dosiahnutý kritický, prípadne nadkritický stav s okamžitými neutrónmi, vtedy sa reaktor rozbieha s periódou určovanou okamžitými neutrónmi. Je samozrejmé, že takýto stav je z hľadiska bezpečnej prevádzky reaktora neprijateľný.

 

12.6.2 Rovnice kinetiky s uvážením vplyvu oneskorených neutrónov

 

  Z predošlého vyplýva, že vplyv oneskorených neutrónov na prechodový proces v reaktore nemožno zanedbať. Na kinetiku reaktora vplývajú aj diferenciálne rovnice popisujúce časový priebeh koncentrácie materských jadier , emitujúcich pri  rozpade oneskorené neutróny.

Za jednotku času sa v jednotke objemu rozpadne  materských jadier, súčastne vznikne  neutrónov pri štiepení jadier uránu alebo plutónia. Na každý štiepny neutrón sa v priemere uvoľní  oneskorených neutrónov. Pri štiepení takto každú sekundu v jednotke objemu vznikne  nových predchodcov materských jadier oneskorených neutrónov. Pre rýchlosť zmeny koncentrácie predchodcov materských jadier môžeme zapísať vzťah

                                          (12.104)

kde  je rozpadová konštanta predchodcov materských jadier i-tej skupiny oneskorených neutrónov.

Hustota toku neutrónov v (12.104) je určená difúznou rovnicou. Zdroj neutrónov v tejto difúznej rovnici je tvorený súčtom okamžitých a oneskorených neutrónov všetkých skupín t.j.

                   (12.105)

Nestacionárna jednoskupinová difúzna rovnica má teda nasledovný tvar

   (12.106)

Priestorové rozloženie hustoty toku neutrónov a koncentrácie predchodcov materských jadier oneskorených neutrónov sa počas prechodového procesu nemení, t.j. platí

                                              (12.107)

Rozloženie hustoty toku neutrónov  je obecne určené superpozíciou priestorovo nezávislých (12.89) t.j.

Vplyv vyšších harmonických zložiek však zanikne už po uplynutí niekoľkých stredných dôb života okamžitých neutrónov  od doby vzniku lokálnej poruchy a priestorové rozloženie hustoty toku neutrónov je dostatočne presne popísané základným (asymptotickým) priebehom . Dosadením (12.107) do (12.106)  obdržíme

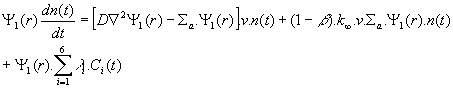       (12.108)

                                 (12.109)

Rovnice (12.108) a (12.109) podelíme  a upravíme

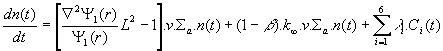         (12.110)

                                                              (12.111)

Vo vzťahu (12.110) je pomer , potom táto rovnica  bude mať tvar

                      (12.112)

Nakoľko rovnice (12.104) až (12.112) sú zapísané pre tepelnú skupinu neutrónov a sústavu konečných rozmerov vystupuje v nich (skryto) pravdepodobnosť neuniknutia neutrónov okamžitých aj oneskorených zo sústavy v procese spomaľovania . Tu sa uvažuje rovnaké  pre okamžité i oneskorené neutróny, čím dochádza v tomto modeli k zvýšeniu úniku oneskorených neutrónov zo sústavy. Túto skutočnosť musíme korigovať použitím . Pričom

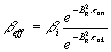                                                                                            (12.113)

Preto odteraz budeme namiesto  používať vo všetkých nasledujúcich vzťahoch . Pri úpravách vzťahov (12.112) a (12.111) použijeme známe

Na základe uvedeného upravíme (12.111) a (12.112) nasledovne

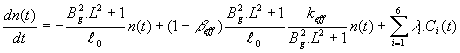     (12.114)

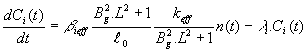                                           (12.115)

Ďalej

                                          (12.116)

                                                                    (12.117)

Rovnicu (12.116) na pravej strane upravíme nasledovne

                                                    (12.118)

                                                                    (12.119)

Ak rovnice (12.118) a (12.119) vynásobíme , potom obdržíme rovnice, ktoré popisujú zmenu hustoty výkonu reaktora nakoľko  a súčin  označíme .

Takto upravené rovnice majú tvar

                                                   (12.120)

                                                                   (12.121)

Rovnice (12.120) a (12.121) predstavujú „deštruktívne“ vyjadrenie kinetických rovníc reaktora. Ak zavedieme do rovníc (12.120) a (12.121) strednú dobu vzniku okamžitých neutrónov  a reaktivitu , definovaných vzťahmi

                                                                                    (12.122)

Po dosadení do kinetických rovníc (12.120) a (12.121) obdržíme

                                                                       (12.123)

                                                                         (12.124)

Nakoľko  je prevrátená hodnota pravdepodobnosti zániku neutrónov a  je reciproká hodnota pravdepodobnosti vzniku okamžitých neutrónov, nazýva sa vyjadrenie kinetických rovníc s  „deštruktívnym“ a vyjadrenie s  „produkčné“.

Obe vyjadrenia kinetických rovníc sú rovnocenné, obe sú široko používané, praktický rozdiel spočíva iba v tom, že v prvom prípade sa zanedbáva, časová závislosť  a v druhom prípade časová závislosť .

Ak poznáme počiatočné podmienky môžeme riešiť rovnice kinetiky numericky. Za tým účelom zintegrujeme rovnicu (12.124) nasledovne

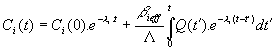                                                   (12.125)

Ak teraz do (12.123) dosadíme namiesto  vzťah (12.125) obdržíme kinetickú rovnicu v integrodiferenciálnom tvare

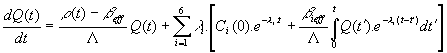        (12.126)

V obecnom prípade závisí  od výkonu reaktora, čím sa kinetické rovnice stávajú nelineárnymi. Potiažou pri riešení (12.126) je i široký rozsah časových hodnôt charakterizujúcich prechodové procesy. Najmenšie hodnoty sú rovnakého rádu ako , t.j. 10-6 až 10-5 s, najväčšie sú dané strednou dobou života poslednej skupiny oneskorených neutrónov, ktorá sa rovná 56 s.