14. Poruchová teória
Malé zmeny neutrónovo - fyzikálnych charakteristík celého
reaktora alebo aj veľké zmeny v malej časti objemu reaktora sa
nazývajú poruchami. Poruchy môžu byť spôsobené zavezením do
reaktora: paliva, absorbátora alebo látky silne rozptyľujúcej neutróny
či ich vybratie z reaktora, zmena teploty, zmena izotopického zloženia a
podobne.
Pod poruchou môžeme rozumieť reálne pôsobenie, napr.
premiestnenie kazety HRK ako aj fiktívne pôsobenie napr. zmeny kroku mreže pri
hľadaní optimálneho usporiadania štiepneho systému.
Aj v tom prípade ak poruchy majú jednoduchý charakter (napr.
sú rovnomerne rozmiestnené v objeme reaktore) a ich vplyv na parametre reaktora
možno oceniť opakovaním výpočtov, úplne analogických výpočtom
reaktora pred poruchová, je jednoduchšie a často aj presnejšie použitie
poruchovej teórie.
Ak poruchy veľmi komplikujú výpočtový model (napr. vznikajú ďalšie hranice, ktoré vyvolávajú zmeny hustoty toku neutrónov pozdĺž súradníc, ktoré predtým nebolo potrebné uvažovať pri výpočte), potom použitie poruchovej teórie uľahčí a zjednoduší výpočet.
Poruchová teória je dobre rozpracovaná v matematickej fyzike, je založená na rozložení riešenia rovníc a vlastného čísla do radu podľa parametra poruchy.
Najčastejšie sa v teórii reaktorov používa člen
prvého rádu malosti a pod poruchovou teóriou rozumieme prvé priblíženie obecnej
teórie.
Pre názornosť rozoberieme niekoľko jednoduchých
úloh, ktoré vytvoria predstavu o poruchách, poruchovej teórii a technike jej
použitia.
Majme kritický homogénny reaktor bez reflektora.
Diferenciálna rovnica popisujúca rozloženie hustoty toku neutrónov ![]() v jednoskupinovom
priblížení s odpovedajúcou okrajovou podmienkou má tvar
v jednoskupinovom
priblížení s odpovedajúcou okrajovou podmienkou má tvar
![]() (14.1)
(14.1)
Podmienka na hranici ![]() (14.2)
(14.2)
Predpokladajme, že reaktor obsahuje poruchu v podobe malých
zmien všetkých parametrov rovnice (14.1) ľubovolne rozložených po celom
objeme reaktora, t.j. ![]() . Nech sú tieto zmeny nezávislé, tak napríklad
. Nech sú tieto zmeny nezávislé, tak napríklad ![]() pri
pri ![]() aj vtedy keď je
aj vtedy keď je![]() . V obecnom prípade bude hustota toku neutrónov v reaktore so
zmenenými parametrami, funkciou času, t.j. reaktor už nebude v kritickom
stave.
. V obecnom prípade bude hustota toku neutrónov v reaktore so
zmenenými parametrami, funkciou času, t.j. reaktor už nebude v kritickom
stave.
Diferenciálna rovnica pre hustotu toku neutrónov v reaktore
s poruchou bude mať tvar
![]() (14.3)
(14.3)
Okrajová podmienka sa zachová t.j. ![]() . (14.4)
. (14.4)
Za nejaký čas od vnesenej poruchy sa zmena hustoty toku
neutrónov ustáli na exponenciálnej funkcii závislej od času.
![]() (14.5)
(14.5)
kde T je ustálená perióda reaktora, ![]() - časová
konštanta. Potom má rovnica (14.3) tvar
- časová
konštanta. Potom má rovnica (14.3) tvar
![]() (14.6)
(14.6)
Vynásobme teraz rovnicu (14.6) hustotou toku neutrónov ![]() , rovnicu (14.1) hodnotou
, rovnicu (14.1) hodnotou ![]() , navzájom ich odčítajme a integrujme po objeme reaktora
V vo vnútri R.
, navzájom ich odčítajme a integrujme po objeme reaktora
V vo vnútri R.
![]() (14.7)
(14.7)
![]() (14.8)
(14.8)
odčítajme
(14.8) od (14.7) a integrujeme po objeme V:
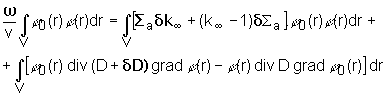 (14.9)
(14.9)
Ak
sú zmeny parametrov ![]() a
a ![]() malé, potom možno
zanedbať člen
malé, potom možno
zanedbať člen ![]() , ktorý je druhou mocninou malých zmien. Druhý integrál na
pravej strane (9) rozpíšeme a upravíme
, ktorý je druhou mocninou malých zmien. Druhý integrál na
pravej strane (9) rozpíšeme a upravíme
![]() (14.10)
(14.10)
Potom bude mať (14.9) tvar

Za
účelom transformácie dvoch posledných integrálov v (14.11) použijeme
Greenovú vetu.
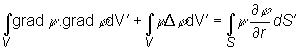 (14.12)
(14.12)
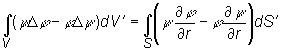 (14.13)
(14.13)
kde
V je objem ohraničený povrchom S,
![]() sú
ľubovoľné funkcie, jednoznačné a spojité na V a S,
sú
ľubovoľné funkcie, jednoznačné a spojité na V a S,
![]() sú derivácie v smere
vonkajšej normály k elementu povrchu dS
sú derivácie v smere
vonkajšej normály k elementu povrchu dS
Zo
vzťahu (14.13) a hraničných podmienok pre ![]() vyplýva rovnosť
posledného integrálu, na pravej strane (11), nule. Druhý integrál na pravej
strane (14.11) upravíme nasledovne
vyplýva rovnosť
posledného integrálu, na pravej strane (11), nule. Druhý integrál na pravej
strane (14.11) upravíme nasledovne
![]() (14.14)
(14.14)
Zo
vzťahu (14.12) a hraničných podmienok vyplýva rovnosť nule,
integrálu cez povrch hranice reaktora, potom platí:
![]() (14.15)
(14.15)
![]() Použitím (14.16) potom pre (14.14) platí:
Použitím (14.16) potom pre (14.14) platí:
![]() (14.17)
(14.17)
Takto
má rovnica (14.11) nasledovný tvar
![]() Doteraz malosť porúch bola potrebná len na neveľké
zjednodušenie obdržaných výsledkov pri prechode od (14.16) k (14.7). Základný
dôsledok predpokladu o malosti porúch je možnosť zámeny
Doteraz malosť porúch bola potrebná len na neveľké
zjednodušenie obdržaných výsledkov pri prechode od (14.16) k (14.7). Základný
dôsledok predpokladu o malosti porúch je možnosť zámeny ![]() vo vzťahu
(14.18) funkciou
vo vzťahu
(14.18) funkciou ![]() . Práve táto zámena robí poruchovú teóriu najefektívnejšou
metódou výpočtu reaktora s meniacimi sa parametrami.
. Práve táto zámena robí poruchovú teóriu najefektívnejšou
metódou výpočtu reaktora s meniacimi sa parametrami.
Preto
budeme predpokladať, že zmeny D, ![]() a
a ![]() sú natoľko malé,
že nespôsobujú podstatnú zmenu
sú natoľko malé,
že nespôsobujú podstatnú zmenu ![]() oproti
oproti ![]() . Potom, zámenou
. Potom, zámenou ![]() na
na ![]() v (14.18) obdržíme
v (14.18) obdržíme
![]() (14.19)
(14.19)
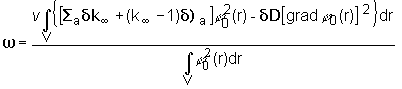 (14.20)
(14.20)
Oceníme
teraz zmenu efektívneho multiplikačného koeficientu ![]() ako dôsledok malých
zmien parametrov
ako dôsledok malých
zmien parametrov ![]() . Preto si predstavme, že do pôvodne kritického reaktora sme
vniesli jedinú poruchu v podobe malej zmeny
. Preto si predstavme, že do pôvodne kritického reaktora sme
vniesli jedinú poruchu v podobe malej zmeny ![]() v celom objeme
rovnomerne rozloženej.
v celom objeme
rovnomerne rozloženej.
Vyberme
také ![]() aby sme obdržali
pôvodnú hodnotu časovej konštanty
aby sme obdržali
pôvodnú hodnotu časovej konštanty ![]() . Potom zo vzťahu (20) pri
. Potom zo vzťahu (20) pri ![]() a
a ![]() vyplýva:
vyplýva:
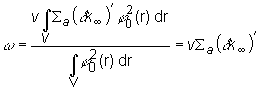 (14.21)
(14.21)
Ak (21) nasledovne upravíme, obdržíme:
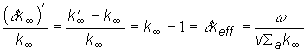 (14.22)
(14.22)
Rovnosť
hodnôt efektívneho multiplikačného koeficientu v reaktoroch s poruchami
rôzneho druhu, vyplýva z rovnosti časovej konštanty ![]() .
.
S
uvážením (14.22), potom (14.20) má tvar
 (14.23)
(14.23)
Posledný vzťah možno zapísať aj v inom tvare, pretože
![]() a
a ![]()
Potom platí
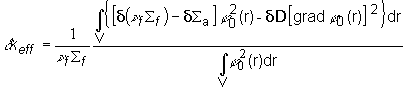 (14.24)
(14.24)
Vzťahy
(14.20), (14.23) a (14.24) predstavujú základné výsledky použitia poruchovej
teórie v jednoskupinovom priblížení.
Niekedy
je nevyhnutnosť určiť vzťah medzi súčastne
prebiehajúcimi zmenami niekoľkých jadrovo-fyzikálnych charakteristík,
počas ktorých zostáva reaktor v kritickom stave. Vzťahy takéhoto
druhu možno obdržať pomocou vzťahu (14.20), ak si uvedomíme, že v
kritickom stave sa časová konštanta ![]() rovná nule.
rovná nule.
Nech
napr. je potrebné určiť pri akej poruche ![]() rovnomerne
rozmiestnenej po objeme AZ, reaktor zostane v kritickom stave, ak zmena
difúzneho koeficientu
rovnomerne
rozmiestnenej po objeme AZ, reaktor zostane v kritickom stave, ak zmena
difúzneho koeficientu ![]() spôsobila zmenu
parametra D. Zo vzťahu (14.20) obdržíme:
spôsobila zmenu
parametra D. Zo vzťahu (14.20) obdržíme:
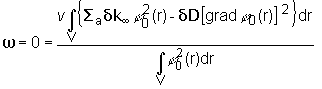 (14.25)
(14.25)
Potom platí:
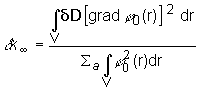
Je zaujímavé, že ak je rozloženie poruchy ![]() rovnomerne rozložené
po objeme reaktora obdržíme:
rovnomerne rozložené
po objeme reaktora obdržíme:
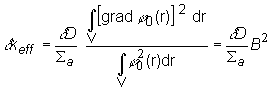 (14.26)
(14.26)
Vzťah
(14.26) platný pre rovnomerné rozloženie poruchy ![]() po reaktore môžeme
získať aj bez použitia poruchovej teórie, nasledovne. Skutočne,
geometrický parameter reaktora pred poruchou
po reaktore môžeme
získať aj bez použitia poruchovej teórie, nasledovne. Skutočne,
geometrický parameter reaktora pred poruchou ![]() je rovný
materiálovému parametru
je rovný
materiálovému parametru ![]() , t.j.
, t.j.
![]() (14.27)
(14.27)
Preto
sa pre kritický reaktor ![]() a pre
a pre ![]() platí:
platí:
![]() (14.28)
(14.28)
a
pre diferenciál zmeny ![]() platí:
platí:
![]() (14.29)
(14.29)
Tento príklad názorne ukazuje, že poruchová teória je cenná ako metóda, pomocou ktorej môžeme jednoducho riešiť úlohy s nerovnomerne rozloženými zmenami parametrov po objeme reaktora.
Doteraz
sme skúmali reaktor s poruchami parametrov nachádzajúcimi sa v jeho celom
objeme. Je zrejmé, že obdržané vzťahy (14.20), (14.23) a (14.24) je možné
použiť aj v prípade porušenia parametrov reaktora len určitej
ohraničenej časti objemu AZ V1. Podmienkou použitia
uvedených vzťahov je, aby aj v tomto prípade bola porucha efektívneho
multiplikačného koeficientu ![]() malá a slabo sa
menilo aj rozloženie hustoty toku neutrónov v ľubovoľnej oblasti
objemu reaktora, t.j.
malá a slabo sa
menilo aj rozloženie hustoty toku neutrónov v ľubovoľnej oblasti
objemu reaktora, t.j.
![]() (14.30)
(14.30)
Posledná podmienka je obzvlášť dôležitá pri riešení úloh so silnými zmenami vlastností rektora vo veľmi malom objeme.
V
takýchto prípadoch, použitím poruchovej teórie všeobecnosti nie je možné
obdržať presné výsledky ani ak je zmena efektívneho multiplikačného
koeficientu malá. Hustota toku neutrónov sa v oblasti poruchy mení podstatne,
preto zámena ![]() na
na ![]() v tejto oblasti nie
je korektná.
v tejto oblasti nie
je korektná.
Pri
splnení podmienok malosti ![]() a
a ![]() sú vyššie uvedené
úvahy platné, je však navyše potrebné uvážiť aj skutočnosť, že
časová konštanta
sú vyššie uvedené
úvahy platné, je však navyše potrebné uvážiť aj skutočnosť, že
časová konštanta ![]() sa líši od nuly v
dôsledku zmien vlastností len v oblasti objemu reaktora V1. V praxi
sa stretávame so zmenou jedného z parametrov
sa líši od nuly v
dôsledku zmien vlastností len v oblasti objemu reaktora V1. V praxi
sa stretávame so zmenou jedného z parametrov ![]() v niektorých
častiach reaktora. Nech napríklad, do oblasti objemu V1
kritického reaktora zanesieme dodatočný absorbátor s makroskopickým
účinným prierezom
v niektorých
častiach reaktora. Nech napríklad, do oblasti objemu V1
kritického reaktora zanesieme dodatočný absorbátor s makroskopickým
účinným prierezom ![]() . Následne sa reaktor dostane do podkritického stavu. Zmenu
jeho efektívneho multiplikačného koeficientu je možné jednoducho
oceniť pomocou vzťahu (29). Potom pre
. Následne sa reaktor dostane do podkritického stavu. Zmenu
jeho efektívneho multiplikačného koeficientu je možné jednoducho
oceniť pomocou vzťahu (29). Potom pre ![]() , platí:
, platí:
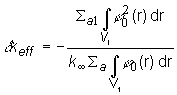 (14.31)
(14.31)
Vo vzťahu (14.31) znamienko mínus znamená, že pri zvýšení absorpcie sa efektívny multiplikačný koeficient zmenší. V matematickom aparáte poruchovej teórie sa pomer (14.32)
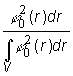 (14.32)
(14.32)
nazýva
štatistickou váhou diferenciálu objemu dr. Potom štatistická váha objemu
V1 je rovná:
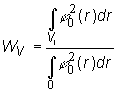 (14.33)
(14.33)
Po
zavedení pojmu štatistická váha objemu V1 môžeme vzťah (14.31)
zapísať nasledovne:
![]() (14.34)
(14.34)
Rozoberme
ešte ďalší veľmi dôležitý prípad použitia poruchovej teórie. Nech je
potrebné určiť efektívny multiplikačný koeficient reaktora s
parametrami závislými od súradníc. Výpočty potrebné na určenie zmeny ![]() klasickým spôsobom je
podstatne názornejší ako analogické výpočty v homogénnom reaktore. Ak je
nehomogenita reálneho reaktora malá, potom s pomocou poruchovej teórie je možné
nehomogénny nahradiť ekvivalentným homogénnym štiepnym systémom.
klasickým spôsobom je
podstatne názornejší ako analogické výpočty v homogénnom reaktore. Ak je
nehomogenita reálneho reaktora malá, potom s pomocou poruchovej teórie je možné
nehomogénny nahradiť ekvivalentným homogénnym štiepnym systémom.
Nech
napr. riešime reaktor s efektívnym multiplikačným koeficientom závislým od
súradníc. Difúzna rovnica kvázi kritického reaktora pre takýto reaktor má tvar:
![]() (14.35)
(14.35)
Nahradíme
tento reaktor iným s tými istými parametrami ![]() , ale s konštantným (nemenným) multiplikačným
koeficientom v celom objeme reaktora
, ale s konštantným (nemenným) multiplikačným
koeficientom v celom objeme reaktora ![]() tak, aby
diferenciálna rovnica difúzie kvázi kritického reaktora mala tvar:
tak, aby
diferenciálna rovnica difúzie kvázi kritického reaktora mala tvar:
![]() (14.36)
(14.36)
Ako
v predchádzajúcom budeme uvažovať, že je splnená podmienka (14.30). Potom,
formálne môžeme uvažovať reaktor s nemenným multiplikačným
koeficientom ![]() , ako reaktor s malou zmenou
, ako reaktor s malou zmenou ![]() pôvodný reaktor. Pre
kritický reaktor potom platí:
pôvodný reaktor. Pre
kritický reaktor potom platí:
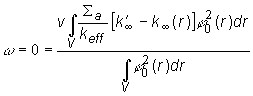 (14.37)
(14.37)
alebo po úprave (14.37):
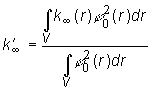 (14.38)
(14.38)
Takto
výpočet efektívneho multiplikačného koeficientu možno robiť pre
homogénny reaktor s multiplikačným koeficientom určeným stredovaným ![]() so štatistickou váhou
diferenciálu objemu dr (14.33).
so štatistickou váhou
diferenciálu objemu dr (14.33).