9. Homogénny reaktor s reflektorom

 

9.1 Vlastnosti reflektora

 

Materiál reflektora tvorí látka, ktorá účinne rozptyľuje neutróny. Časť takto rozptýlených neutrónov sa vracia späť do AZ, tým reflektor znižuje únik neutrónov z AZ. Pretože únik neutrónov sa zmenšil, pre dosiahnutie kritického stavu musíme použiť sústavu s menšími rozmermi. Takto sme ušetrili štiepny materiál a zvýšili jeho merný výkon. Okrem už uvedeného, hustota toku neutrónov v hraničnej oblasti stúpne v porovnaní s reaktorom holým. Pretože výkon reaktora je úmerný hustote toku neutrónov, bude i výkon v AZ rovnomernejší. Zmena hustoty toku neutrónov v reflektore bude vysvetlená neskoršie.

Podmienky pre materiál reflektora sú : veľký  a veľmi malý .


Čím menšia je , tým väčšia je pravdepodobnosť, že neutrón rozptýlený v reflektore sa z hĺbky opäť vráti do AZ.

 


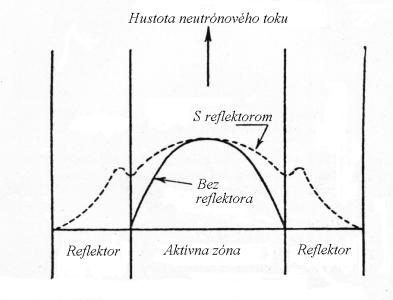
Obr. 9.1 Rozloženie hustoty toku neutrónov v reaktore bez reflektora a s reflektorom

 

1) Ako bolo povedané pri zachovaní  sa dosiahne stavu kritičnosti v podstatne menších rozmeroch AZ pre reaktor s reflektorom, ako pre reaktor holý.

2) Prítomnosť reflektora zvýši úroveň hustoty toku tepelných neutrónov v periferickej oblasti. Tým sa čiastočne vyrovná hustote toku neutrónov v AZ a zvýši sa stredná hodnota hustoty toku neutrónov pri nezmenenej , to znamená, že výkon reaktora tiež vzrástol.

3) V reaktore s reflektorom sú obvodové miesta AZ podstatne viac využité ako v prípade holého reaktora.

 

9.2 Požiadavky na reflektor

 

Čím má byť väčšia pravdepodobnosť, že neutrón po rozptyle ( izotropnom ) v reflektore sa vráti do AZ, tým musí byť  menšie. Pretože pri izotropnom rozptyle je pravdepodobnosť rozptylu do určitého smeru priamoúmerná priestorovému uhlu. Teda čím je  menšia, tým väčší je priestorový uhol, pod ktorým rozptýlený neutrón vidí AZ. Keď je  malá, bude malý aj koeficient difúzie D.

Ak je malá , potom pravdepodobnosť, že neutrón vracajúci sa do AZ, bude absorbovaný, je menšia. (- pravdepodobnosť, že neutrón bude absorbovaný na úseku x, x + dx.)

Nakoľko prevažná časť neutrónov unikla z AZ počas spomaľovania, teda neutróny, ktoré unikajú sú nadtepelné, bolo by výhodné, keby sa do AZ vracali ako tepelné. Toto je možné, len ak reflektor bude mať veľkú moderačnú spôsobilosť , teda bude to dostatočne ľahký materiál a súčasne jeho  bude malé.

Teoretický výpočet reaktora s reflektorom je zložitou úlohou. V reaktore bez reflektora je hustota spomaľovania v každom bode AZ  úmerná hustote toku tepelných neutrónov. Rovnica difúzie je potom lineárna a homogénna, ktorú je možné pomerne jednoducho riešiť. Pretože reflektor má obecne iné množivé a moderačné vlastnosti ako AZ, preto sa energetické spektrum neutrónov, ktoré je u holého reaktora všade rovnaké, podstatne mení v blízkosti rozhrania AZ s reflektorom. Tým sa zvyšuje obtiažnosť riešenia rovnice stárnutia ( Fermiho-Amaldiho rovnice ). Riešenie tejto rovnice predstavuje zdroje tepelných neutrónov v difúznej rovnici. Jedným zo spôsobov ako zjednodušiť rozbor spomaľovania neutrónov v reaktore s viacerými oblasťami, je metóda skupín alebo grupová metóda. Pri tomto sa predpokladá, že energia neutrónov od E0 = 2 MeV až do tepelnej ETh = 0.0253 eV sa rozdelí na konečný počet menších intervalov energie, teda neutróny sa podľa energie rozdelia do skupín. Predpokladáme, že neutróny každej skupiny difundujú bez straty energie tak dlho, až vykonajú priemerný počet zrážok, ktorý je potrebný, aby ich energia klesla na energiu nasledujúcej nižšej skupiny. Predpokladáme, že spomaľujúci neutrón postupne prejde skokom cez všetky skupiny neutrónov od E0 = 2 MeV až do ETh = 0.0253 eV.

 

9.3 Jedna skupina neutrónov

 

Toto zjednodušenie nepredpokladá existenciu rýchlych neutrónov, teda pravdepodobnosť úniku rezonančného zachytenia p, koeficient rozmnoženia na rýchlych neutrónoch, budú rovné jednej, teda .

 

Označme indexom “a” všetky konštanty a hustotu toku neutrónov v AZ, a indexom “r” konštanty a hustotu toku neutrónov v reflektore.

 

Potom môžeme zapísať rovnicu difúzie v oboch prostrediach v stacionárnom stave. Pre aktívnu zónu bude platiť:

                                    (9.14)

                                            (9.15)

                                             (9.16)

- materiálový parameter AZ.

 - toto približne upresníme, ak namiesto  položíme , kde

kde - kvadrát difúznej dĺžky v aktívnej zóne

       - Fermiho vek neutrónov pre aktívnu zónu

       - kvadrát migračnej dĺžky v aktívnej zóne

Pre reflektor, kde niet zdrojov neutrónov, bude platiť:

                                                    (9.17)

                                                         (9.18)

        (9.19)                                                           (9.20)

kde Lr je difúzna dĺžka v reflektore.


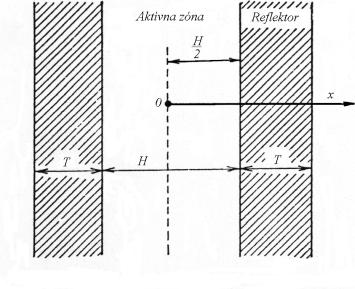
Riešme teraz diferenciálne rovnice 9.16 a 9.18 pre AZ v tvare nekonečnej dosky, obklopenej reflektorom.

 


Obr. 9.2 Reaktor v tvare nekonečnej dosky s reflektorom

 

Hrúbka reflektora je vrátane extrapolovanej dĺžky. Riešenie rovníc 9.16 a 9.18 pre doskovú AZ zapíšeme v tvare:

                                                     (9.21)

A - ľubovoľná konštanta

                                         (9.22)

Na extrapolovanej vzdialenosti vo vákuu je hustota neutrónov rovná nule, t.j:

                                                                                              (9.23)

Potom:

  (9.24)

Zo vzťahu 9.24 vyjadríme konštantu :

                              (9.25)

Pre hustotu toku neutrónov v reflektore môžeme napísať vzťah:

             (9.26)

Ďalšou úpravou získame vzťah pre

           (9.27)

                                   (9.28)

Pri úprave sme využili nasledovné vzťahy:

      

 

Vzťah medzi integračnými konštantami A, C dostaneme z druhej okrajovej podmienky:

Na rozhraní AZ a reflektora pri  sa musia navzájom rovnať hustoty tokov neutrónov a hustoty prúdu neutrónov.

                                          (9.29)

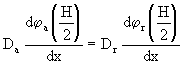                                      (9.30)

 

Z podmienky 9.29 platí

                                     (9.31)

                                            (9.32)

Z podmienky 9.30 platí

                                 (9.33)

                                      (9.34)

Ak podelíme vzťah 9.34 rovnicou 9.32 obdržíme:

                                       (9.35)

Táto rovnica je podľa jednoskupinovej teórie kritickou rovnicou reaktora tvoreného nekonečnou doskou a reflektorom o hrúbke T. Rovnica je vzhľadom na  transcendentnou rovnicou. Nakoľko veličiny ,, a  môžeme určiť, ak poznáme materiál, z ktorého je sústava vytvorená a poznáme súčasne vzájomný pomer materiálov. Potom podľa kritickej rovnice môžeme vyjadriť hrúbku H pri známom T, alebo T pri známom H tak, aby sústava bola kritická.

      alebo 

Pre hrúbku reflektora T je možné stanoviť, že s počiatočným zväčšovaním hrúbky T prudko rastie úspora získaná reflektorom, avšak pri väčších hodnotách T sa rast úspory zmenšuje až pri  sa rast úspory zastaví. Pre T = 0 bude reaktor holý, preto  určíme z nasledujúceho: teda  to vtedy, ak    - čo je geometrický parameter pre holý reaktor.

 

 

9.4 Úspora získaná reflektorom

 

Úspora získaná reflektorom je daná výrazom:

                                                   (9.36)

kde H0 je kritický rozmer holej AZ.

Ukázali sme si, že  potom pre úsporu získanú reflektorom platí:

                                                  (9.37)

alebo                                                                                                                (9.38)

Ak do kritickej rovnice 9.35 dosadíme vzťah 9.38, obdržíme:

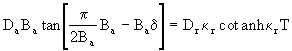                       (9.39)

Po úprave

                                (9.40)

Pri úprave 9.40 použijeme

                                                 (9.41)

takže platí:

                                      (9.42)

                                              (9.43)

                                                      (9.44)

Úsporu získanú reflektorom určíme:

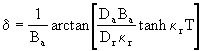                                             (9.45)

V prípade, že hrúbka reflektora bude malá, alebo H0 bude veľké, tomu zodpovedajúce Ba bude malé, potom  bude malé číslo, preto  môžeme zapísať . Pre vzťah 9.44 môžeme potom zapísať:

                                            (9.46)

Úspora získaná reflektorom pre veľkú AZ má tvar:

;                                                 (9.47)

                                                     (9.48)

Ak Da = Dr , ptom .

Ak je difúzna dĺžka Lr podstatne väčšia ako T, potom pre:

                                                (9.49)

teda úspora získaná reflektorom pri malých hrúbkach T je priamoúmerná hrúbke reflektora. Ak naopak hrúbka reflektora bude v porovnaní z Lr veľká, potom:

        a                                                  (9.50)

Toto je hraničná hodnota úspory získanej reflektorom , ktorá nezávisí od hrúbky reflektoraT.